题目内容
将函数y=
sinx+
cosx(x∈R)的图象向左平移m(m>0)个单位长度后,所得到的图象关于y轴对称,则m的最小值是( )
| 1 |
| 4 |
| ||
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:两角和与差的正弦函数,函数y=Asin(ωx+φ)的图象变换
专题:计算题,三角函数的图像与性质
分析:用两角和与差的三角函数化简函数y=
cos(x-
),通过图象的平移,得到函数的表达式,由函数图象关于y轴对称,函数在y轴处取得函数的最值,求解即可
| 1 |
| 2 |
| π |
| 6 |
解答:
解:函数y=
sinx+
cosx=
cos(x-
),图象向左平移m个单位可得y=
cos(x+m-
),
根据偶函数的性质:图象关于y轴对称,故可得此函数在y轴处取得函数的最值,
即cos(x+m-
)=±1,
解得,m-
=kπ,
∴m=kπ+
,k∈Z,
∵m>0,
∴k=0时,m的最小值为
.
故选:B.
| 1 |
| 4 |
| ||
| 4 |
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
根据偶函数的性质:图象关于y轴对称,故可得此函数在y轴处取得函数的最值,
即cos(x+m-
| π |
| 6 |
解得,m-
| π |
| 6 |
∴m=kπ+
| π |
| 6 |
∵m>0,
∴k=0时,m的最小值为
| π |
| 6 |
故选:B.
点评:本题将三角函数图象向左平移m个单位,所得图象关于y轴对称,求m的最小值.着重考查了三角函数的化简、三角函数图象的对称性等知识,属于基础题.

练习册系列答案
相关题目
已知在△ABC中满足:tanA•tanB=1+
(tanA+tanB),则角C等于( )
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
三个数a=60.7,b=0.76,c=log0.76的大小顺序是( )
| A、a<b<c |
| B、c<b<a |
| C、c<a<b |
| D、a<c<b |
在△ABC中,已知sin(
-A)cosB>sinAsin(π-B),则△ABC是( )
| π |
| 2 |
| A、钝角三角形 |
| B、直角三角形 |
| C、锐角三角形 |
| D、等腰三角形 |
椭圆的长轴为6,短轴为4,则椭圆的标准方程是( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
| D、以上都不是 |
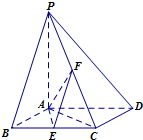 如图,已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
如图,已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.