题目内容
设集合M={x|lnx>0},N={x|-3≤x≤3},则M∩N=( )
| A、(1,3] |
| B、[1,3) |
| C、(1,3) |
| D、[1,3] |
考点:交集及其运算
专题:集合
分析:解对数不等式可化简M,取交集可得.
解答:
解:∵M={x|lnx>0}={x|x>1}
又∵N={x|-3≤x≤3},
∴M∩N={x|1<x≤3}=(1,3]
故选:A
又∵N={x|-3≤x≤3},
∴M∩N={x|1<x≤3}=(1,3]
故选:A
点评:本题考查集合的交集,属基础题.

练习册系列答案
相关题目
已知函数f(x)=2x-2,g(x)=-x2+4x-3,若有f(a)=g(b),则b的范围是( )
A、(2-
| ||||
B、[2-
| ||||
| C、(-1,5) | ||||
| D、[-1,5] |
设M是椭圆
+
=1上的一点,F1,F2为焦点,∠F1MF2=
,则△MF1F2的面积为( )
| x2 |
| 25 |
| y2 |
| 16 |
| π |
| 6 |
A、
| ||||
B、16(2+
| ||||
C、16(2-
| ||||
| D、16 |
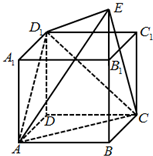 如图长方体ABCD-A1B1C1D1中,底面ABCD是边长为1的正方形,|BB1|=a,E为BB1延长线上的一点且满足|BB1|•|B1E|=1.
如图长方体ABCD-A1B1C1D1中,底面ABCD是边长为1的正方形,|BB1|=a,E为BB1延长线上的一点且满足|BB1|•|B1E|=1.