题目内容
设M是椭圆
+
=1上的一点,F1,F2为焦点,∠F1MF2=
,则△MF1F2的面积为( )
| x2 |
| 25 |
| y2 |
| 16 |
| π |
| 6 |
A、
| ||||
B、16(2+
| ||||
C、16(2-
| ||||
| D、16 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:根据椭圆的定义和余弦定理建立关于m、n的方程组,平方相减即可求出|PF1|•|PF2|,结合三角形的面积公式,可得△MF1F2的面积
解答:
解:∵椭圆方程为
+
=1上的一点,F1,F2为焦点,∠F1MF2=
,
∴a2=25,b2=16,可得c2=a2-b2=9,即a=5,c=3,
设|PF1|=m,|PF2|=n,则有m+n=10,
∵∠F1MF2=
,
∴36=m2+n2-2mncos
∵(m+n)2=m2+n2+2mn,
∴mn=
,
∴|PF1|•|PF2|=
.
∴△PF1F2的面积S=
|PF1|•|PF2|sin
=
•
•
=16(2-
).
故选:C.
| x2 |
| 25 |
| y2 |
| 16 |
| π |
| 6 |
∴a2=25,b2=16,可得c2=a2-b2=9,即a=5,c=3,
设|PF1|=m,|PF2|=n,则有m+n=10,
∵∠F1MF2=
| π |
| 6 |
∴36=m2+n2-2mncos
| π |
| 6 |
∵(m+n)2=m2+n2+2mn,
∴mn=
| 64 | ||
2+
|
∴|PF1|•|PF2|=
| 64 | ||
2+
|
∴△PF1F2的面积S=
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
| 64 | ||
2+
|
| 1 |
| 2 |
| 3 |
故选:C.
点评:本题给出椭圆的焦点三角形,求它的面积,着重考查了余弦定理、椭圆的定义和简单几何性质等知识.

练习册系列答案
相关题目
设集合M={x|lnx>0},N={x|-3≤x≤3},则M∩N=( )
| A、(1,3] |
| B、[1,3) |
| C、(1,3) |
| D、[1,3] |
曲线
(θ为参数)的对称中心( )
|
| A、在直线y=2x上 |
| B、在直线y=-2x上 |
| C、在直线y=x-3上 |
| D、在直线y=x+3上 |
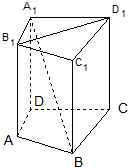 如图,在直四棱柱A1B1C1 D1-ABCD中,当底面四边形ABCD满足条件
如图,在直四棱柱A1B1C1 D1-ABCD中,当底面四边形ABCD满足条件