题目内容
10.在平面直角坐标系xoy中,椭圆C的中心为原点,焦点F1,F2在x轴上,离心率为$\frac{\sqrt{2}}{2}$,与过F1的直线交于A,B两点,且△ABF2的周长为16,那么椭圆C的方程为( )| A. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{8}$=1 | B. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1 | C. | $\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{6}$=1 |
分析 根据题意,作出椭圆的图形分析可得|AB|+|AF2|+|BF2|=|AF1|+|BF1|+|AF2|+|BF2|=4a=16,解可得a的值,又由其离心率可得e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,解可得c的值,计算可得b的值,将a、b的值代入椭圆标准方程即可得答案.
解答 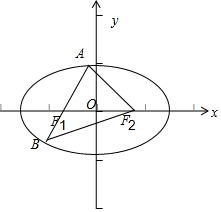 解:根据题意,如图:
解:根据题意,如图:
△ABF2的周长为16,则有|AB|+|AF2|+|BF2|=|AF1|+|BF1|+|AF2|+|BF2|=4a=16,则a=4,
又由其离心率e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,则c=2$\sqrt{2}$,b2=a2-c2=16-8=8;
又由其焦点在x轴上,则其标准方程为$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{8}$=1;
故选:A.
点评 本题考查椭圆的几何性质,关键是由△ABF2的周长求出a的值.属于中档题.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
15.已知函数$f(x)=sin(ωx+φ)(ω>0,|φ|<\frac{π}{2})$,其图象相邻两条对称轴之间的距离为$\frac{π}{2}$,且函数$f(x+\frac{π}{12})$是偶函数,则下列判断正确的是( )
| A. | 函数f(x)的最小正周期为2π | |
| B. | 函数f(x)在区间$[\frac{3π}{4},π]$上单调递增 | |
| C. | 函数f(x)的图象关于直线$x=-\frac{7π}{12}$对称 | |
| D. | 函数f(x)的图象关于点$(\frac{7π}{12},0)$对称 |
2.函数f(x)=9x3-ln|x|的图象大致是( )
| A. |  | B. |  | C. |  | D. |  |
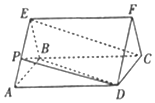 如图,三棱柱ABE-DCF中,△EAB是正三角形,四边形ABCD是矩形,且EA=2,BC=2$\sqrt{3}$,EC=4.
如图,三棱柱ABE-DCF中,△EAB是正三角形,四边形ABCD是矩形,且EA=2,BC=2$\sqrt{3}$,EC=4.