题目内容
18．已知球的直径SC=2$\sqrt{5}$，A，B是该球球面上的两点，若AB=2，∠ASC=∠BSC=45°，则棱锥S-ABC的表面积为（ ）| A． | 22 | B． | 16 | C． | 12 | D． | 10 |
分析 证明SC⊥面ABO，求出各侧面面积，即可求出棱锥S-ABC的表面积．
解答 解：∵∠BSC=∠ASC=45°，且SC为直径，
∴△ASC与△BSC均为等腰直角三角形．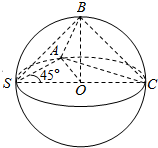
∴BO⊥SC，AO⊥SC．
又AO∩BO=O，∴SC⊥面ABO．
△SAB中，SA=AB=$\sqrt{10}$，AB=2，∴S△SAB=$\frac{1}{2}×2×\sqrt{10-1}$=3，
同理S△ABC=3，
∵S△BSC=S△ASC=$\frac{1}{2}×2\sqrt{5}×\sqrt{5}$=5
∴棱锥S-ABC的表面积为16，
故选：B．
点评 本题考查线面垂直，考查棱锥S-ABC的表面积，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
8．已知定义在R上的可导函数f（x）的导函数为f′（x），满足f′（x）＜f（x），且f（-x）=f（2+x），f（2）=1，则不等式f（x）＜ex的解集为（ ）
| A． | （-2，+∞） | B． | （2，+∞） | C． | （1，+∞） | D． | （0，+∞） |
6．在区间$[-\sqrt{2}，\sqrt{2}]$中随机取一个实数k，则事件“直线y=kx与圆（x-3）2+y2=1相交”发生的概率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{6}$ | D． | $\frac{1}{8}$ |
3．设函数f（x）=x2-2ex-$\frac{lnx}{x}$+a（其中e为自然对数的底数，若函数f（x）至少存在一个零点，则实数a的取值范围是（ ）
| A． | $（{0，{e^2}-\frac{1}{e}}]$ | B． | $（{0，{e^2}+\frac{1}{e}}]$ | C． | $[{{e^2}-\frac{1}{e}，+∞}）$ | D． | $（{-∞，{e^2}+\frac{1}{e}}]$ |
10．在平面直角坐标系xoy中，椭圆C的中心为原点，焦点F1，F2在x轴上，离心率为$\frac{\sqrt{2}}{2}$，与过F1的直线交于A，B两点，且△ABF2的周长为16，那么椭圆C的方程为（ ）
| A． | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{8}$=1 | B． | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1 | C． | $\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1 | D． | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{6}$=1 |
