题目内容
已知向量
=（2，-3，0），
=（k，0，3），若
，
成120°的角，则k= ．
| a |
| b |
| a |
| b |
考点：数量积表示两个向量的夹角
专题：空间向量及应用
分析：由空间向量的数量积定义解答．
解答：
解：由已知，
•
=（2，-3，0）（k，0，3）=
•
cos120°=2k，所以k=-
；
故答案为：-
．
| a |
| b |
| 13 |
| k2+9 |
| 39 |
故答案为：-
| 39 |
点评：本题考查了空间向量的数量积定义以及坐标表示．
练习册系列答案
名校课堂系列答案
相关题目
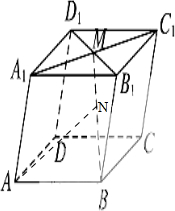如图，在平行六面体ABCD-A1B1C1D1中，点M为A1C1与B1D1的交点，若| A1B1 |
| a |
| A1D1 |
| b |
| A1A |
| c |
| BN |
| NM |
| AN |
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
已知A（1，2，1），B（-1，3，4），P为AB的中点，则|
|=（ ）
| AP |
A、5
| ||||
B、
| ||||
C、
| ||||
D、
|
经统计，数学的学习时间（单位：小时）与成绩（单位：分）近似线性相关关系，对某小组学生每周用于数学的学习时间x与数学成绩y进行数据收集如表
由表中样本数据求的回归方程为
=bx+
，且直线l：x+18y=100，则点（
，
）在直线l的．
| x | 15 | 16 | 18 | 19 | 22 |
| y | 102 | 98 | 115 | 115 | 120 |
 |
| y |
|
| a |
|
| a |
|
| b |
| A、右下方 | B、右上方 |
| C、左下方 | D、左上方 |
设P为曲线C：y=x2-x+3上的点，且曲线C在点P处切线斜率的取值范围为[0，1]，则点P横坐标的取值范围为（ ）
A、[-1，-
| ||
| B、[-1，0] | ||
| C、[0，1] | ||
D、[
|