Question

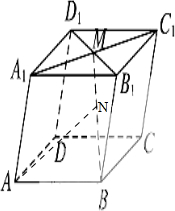如图，在平行六面体ABCD-A₁B₁C₁D₁中，点M为A₁C₁与B₁D₁的交点，若

A1B1

=

a

，

A1D1

=

b

，

A1A

=

c

，点N在BM上，且

BN

=2

NM

，则向量

AN

等于（　　）

• A、

  1

  3

  a

  +

  2

  3

  b

  -

  2

  3

  c

• B、

  2

  3

  a

  +

  1

  3

  b

  -

  2

  3

  c

• C、

  2

  3

  a

  -

  1

  3

  b

  -

  2

  3

  c

• D、

  1

  3

  a

  -

  2

  3

  b

  -

  2

  3

  c

Answer 1

考点：平面向量的基本定理及其意义

专题：平面向量及应用

分析：根据平行四边形的性质与向量的减法法则，再由向量加法的三角形法则，进而得到本题答案．

解答： 解：∵

BN

=2

NM

，
∴

BN

=

2

3

BM

=

2

3

（

BB1

+

B1M

）=

2

3

BB1

+

2

3

×

1

2

（

B1A1

+

B1C1

）=

2

3

BB1

+

1

3

B1A1

+

1

3

B1C1

∴

AN

=

AB

+

BN

=

A1B1

+

2

3

BB1

+

1

3

B1A1

+

1

3

B1C1

=

2

3

A1B1

-

2

3

A1A

-

1

3

A1D1

=

2

3

a

-

2

3

c

-

1

3

b

故选：C．

点评：本题着重考查了平行四边形与平行六面体的性质、向量的定义与加减法则等知识，属于基础题．