题目内容
棱长为3的正方体的外接球（各顶点均在球面上）的表面积为 ．
考点：球的体积和表面积
专题：计算题,空间位置关系与距离,球
分析：由正方体与外接球的关系为正方体的对角线长为球的直径，设球的半径为r，则3
=2r，求出r，再由球的表面积公式计算即可得到．
| 3 |
解答：
解：由正方体与外接球的关系为正方体的对角线长为球的直径，
设球的半径为r，
则3
=2r，解得，r=
．
则球的表面积为S=4πr2=4π×
=27π．
故答案为：27π．
设球的半径为r，
则3
| 3 |
3
| ||
| 2 |
则球的表面积为S=4πr2=4π×
| 27 |
| 4 |
故答案为：27π．
点评：本题考查正方体与外接球的关系，考查球的表面积公式的运用，考查运算能力，属于基础题．
练习册系列答案
相关题目
已知函数f（x）=xa的图象过点（4，2），令an=
，n∈N*，记数列{an}的前n项和为Sn，则S2015=（ ）
| 1 |
| f(n+1)+f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|
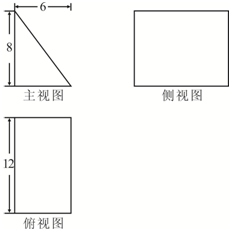一块橡胶泥表示的几何体的三视图如图所示，将该橡胶泥揉成一个底面边长为8的正三角形的三棱锥，则这个三棱锥的高为（ ）A、3
| ||
B、6
| ||
C、9
| ||
D、18
|