题目内容
在△ABC中，sinA：sinB：sinC=4：3：2，那么cosB的值为（ ）
A、
| ||
B、-
| ||
C、
| ||
D、
|
考点：余弦定理,正弦定理
专题：解三角形
分析：由正弦定理可得a：b：c=4：3：2，进而可设a=4x，b=3x，c=2x，（x＞0）代入余弦定理求解可得．
解答：
解：由正弦定理知，
sinA：sinB：sinC=4：3：2可化为，
a：b：c=4：3：2．
∴可设a=4x，b=3x，c=2x，（x＞0）
由余弦定理得，
cosB=
=
=
．
故选：A．
sinA：sinB：sinC=4：3：2可化为，
a：b：c=4：3：2．
∴可设a=4x，b=3x，c=2x，（x＞0）
由余弦定理得，
cosB=
| a2+c2-b2 |
| 2ac |
=
| 16x2+4x2-9x2 |
| 2×4x×2x |
=
| 11 |
| 16 |
故选：A．
点评：本题主要考查正弦定理和余弦定理得应用，解题的关键是设a=4x，b=3x，c=2x，（x＞0）．属于基础题．
练习册系列答案
习题精选系列答案
相关题目
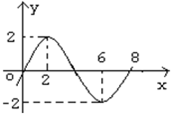函数f（x）=Asin（ωx+ϕ）（A＞0，ω＞0）的部分图象如图所示，则f（1）+f（2）+…+f（11）的值是（ ）A、2+2
| ||
B、2-2
| ||
| C、0 | ||
| D、-1 |
某射击俱乐部四名运动员甲、乙、丙、丁在选拔赛中所得的平均环数
及其方差s2如表所示，若从中选送一人参加决赛，则最佳人选是（ ）
. |
| x |
| 甲 | 乙 | 丙 | 丁 | |||
|
9.1 | 9.3 | 9.3 | 9.2 | ||
| s2 | 5.7 | 6.2 | 5.7 | 6.4 |
| A、甲 | B、乙 | C、丙 | D、丁 |
y=3sinx+
cosx（-
≤x≤
）的值域是（ ）
| 3 |
| π |
| 2 |
| π |
| 2 |
A、（-2
| ||||
B、[-2
| ||||
C、[-3，2
| ||||
D、[-2
|
已知sin(
+x)=
(
＜x＜
)，则式子
的值为（ ）
| π |
| 4 |
| 12 |
| 13 |
| π |
| 4 |
| π |
| 2 |
| cos2x | ||
cos(
|
A、-
| ||
B、
| ||
C、
| ||
D、-
|
方程sinx=-cos80°的解集是（ ）
| A、{X|X=k•180°+10°，k∈z} |
| B、{x|x=k•360°+10°，k∈z} |
| C、{x|x=k•180°±10°，k∈z} |
| D、{x|x=k•180°-（-1）k•10°，k∈z} |