题目内容
已知sin(
+x)=
(
<x<
),则式子
的值为( )
| π |
| 4 |
| 12 |
| 13 |
| π |
| 4 |
| π |
| 2 |
| cos2x | ||
cos(
|
A、-
| ||
B、
| ||
C、
| ||
D、-
|
考点:三角函数中的恒等变换应用
专题:三角函数的求值
分析:由sin(
+x)=
(
<x<
)得,cos(
+x)=-
,从而cos2x=sin(
+2x)=2sin(
+x)cos(
+x)=-
,cos(
-x)=cos[
-(
+x)]=sin(
+x)=
.然后可得出式子
的值.
| π |
| 4 |
| 12 |
| 13 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| 5 |
| 13 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 120 |
| 169 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 12 |
| 13 |
| cos2x | ||
cos(
|
解答:
解:∵sin(
+x)=
(
<x<
),
∴
<
+x<π,
∴cos(
+x)=-
,
∴cos2x=sin(
+2x)
=2sin(
+x)cos(
+x)
=-
,
又∵cos(
-x)=cos[
-(
+x)]
=sin(
+x)=
.
∴
=-
.
故选:A.
| π |
| 4 |
| 12 |
| 13 |
| π |
| 4 |
| π |
| 2 |
∴
| π |
| 2 |
| π |
| 4 |
∴cos(
| π |
| 4 |
| 5 |
| 13 |
∴cos2x=sin(
| π |
| 2 |
=2sin(
| π |
| 4 |
| π |
| 4 |
=-
| 120 |
| 169 |
又∵cos(
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
=sin(
| π |
| 4 |
| 12 |
| 13 |
∴
| cos2x | ||
cos(
|
| 10 |
| 13 |
故选:A.
点评:本题考查诱导公式,倍角公式,不等式的性质等知识的综合应用.属于基础题.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
在复平面内,复数z=
对应的点在( )
| 1-i |
| 1+2i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
若A(-2,3)、B(3,-2)、C(
,m﹚三点在同一直线上,则m的值为( )
| 1 |
| 2 |
| A、-2 | ||
| B、2 | ||
C、-
| ||
D、
|
在△ABC中,sinA:sinB:sinC=4:3:2,那么cosB的值为( )
A、
| ||
B、-
| ||
C、
| ||
D、
|
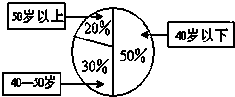 某单位200名职工的年龄分布情况如图,现要从中抽取40名职工作样本,用系统抽样法,将全体职工随机按1-200编号,并按编号顺序平均分为40组(1-5号,6-10号,…,196-200号).若第6组抽出的号码为28,则第8组抽出的号码应是a; 若用分层抽样方法,则50岁以下年龄段应抽取b人.那么a+b等于( )
某单位200名职工的年龄分布情况如图,现要从中抽取40名职工作样本,用系统抽样法,将全体职工随机按1-200编号,并按编号顺序平均分为40组(1-5号,6-10号,…,196-200号).若第6组抽出的号码为28,则第8组抽出的号码应是a; 若用分层抽样方法,则50岁以下年龄段应抽取b人.那么a+b等于( )