题目内容
已知函数f（x）=
，则它们的单调增区间是 ．
|
考点：函数的单调性及单调区间
专题：函数的性质及应用
分析：首先分别求出在不同定义域内的函数的单调区间，进一步求出函数的整体单调区间．
解答：
解：函数f（x）=
根据函数的解析式：当x≥0时，函数的单调递增区间为：[1，+∞）
当x＜0时，函数的单调递增区间为：（-∞，-1]
所以函数的递增区间为：[1，+∞）和（-∞，-1]
故答案为：（-∞，-1]和[1，+∞）
|
根据函数的解析式：当x≥0时，函数的单调递增区间为：[1，+∞）
当x＜0时，函数的单调递增区间为：（-∞，-1]
所以函数的递增区间为：[1，+∞）和（-∞，-1]
故答案为：（-∞，-1]和[1，+∞）
点评：本题考查的知识要点：分段函数的单调性的应用．属于基础题型．
练习册系列答案
应用题作业本系列答案
相关题目
设双曲线
-
=1（a＞0，b＞0）的右焦点为F，过点F作与x轴垂直的直线l交两渐近线于A，B两点，且与双曲线在第一象限的交点为P，设O为坐标原点，若
=λ
+μ
（λ，μ∈R），λ•μ=
，则双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| OP |
| OA |
| OB |
| 3 |
| 16 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
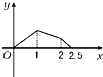
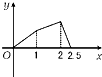
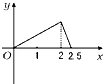
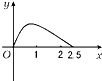
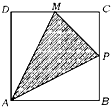如图，点P在边长为1的正方形的边上运动，设M是CD的中点，则当P沿着路径A-B-C-M运动时，点P经过的路程x与△APM的面积y的函数关系为y=f（x），则y=f（x）的图象是
