题目内容
3.现有正整数构成的数表如下:第一行:1
第二行:12
第三行:1123
第四行:11211234
第五行:1121123112112345
…
第k行:先抄写第1行,接着按原序抄写第2行,然后按原序抄写第3行,…,直至按原序抄写第k-1行,最后添上数k.(如第四行,先抄写第一行的数1,接着按原序抄写第二行的数1,2,接着按原序抄写第三行的数1,1,2,3,最后添上数4).
将按照上述方式写下的第n个数记作an(如a1=1,a2=1,a3=2,a4=1,…,a7=3,…,a14=3,a15=4,…)
(1)用tk表示数表第k行的数的个数,求数列{tk}的前k项和Tk;
(2)第8行中的数是否超过73个?若是,用${a_{n_0}}$表示第8行中的第73个数,试求n0和${a_{n_0}}$的值;若不是,请说明理由;
(3)令Sn=a1+a2+a3+…+an,求S2017的值.
分析 (1)根据题意先求出{tk}的通项公式,再根据等比数列的求和公式计算即可,
(2)由${t_k}={2^{k-1}}$得第8行中共有27=128个数,得到第8行中的数超过73个,按上述顺序依次写下的第73个数应是第7行的第73-63=10个数,同上过程知a73=a10=2,即可求出答案,
(3)根据错位相减法求出得${S_{{2^n}-1}}=-n+2+{2^2}+…+{2^{n-1}}+{2^n}$=2n+1-n-2,再逐一展开得到S2017=(211-12)+(210-11)+(29-10)+(28-9)+(27-8)+(26-7)+(24-5),即可求出.
解答 解:(1)当k≥2时,tk=t1+t2+…+tk-1+1,tk+1=t1+t2+…+tk+1,
于是tk+1-tk=t1,即tk+1=2tk,又t2=2t1,t1=1
所以${t_k}={2^{k-1}}$,
故${T_k}=1+2+{2^2}+…+{2^{k-1}}={2^k}-1$.
(2)由${t_k}={2^{k-1}}$得第8行中共有27=128个数,
所以,第8行中的数超过73个,
${n_0}={T_7}+73={2^7}-1+73=200$,
从而,${a_{n_0}}={a_{200}}={a_{73}}$,
由26-2=63<73,27-1=127>73,
所以,按上述顺序依次写下的第73个数应是第7行的第73-63=10个数,同上过程知a73=a10=2,
所以,${a_{n_0}}=2$.
(3)由于数表的前n行共有2n-1个数,于是,先计算${S_{{2^n}-1}}$.
在前2n-1个数中,共有1个n,2个n-1,22个n-2,…,2n-k个k,…,2n-1个1,
因此${S_{{2^n}-1}}=n×1+(n-1)×2+…+k×{2^{n-k}}+$…+2×2n-2+1×2n-1,
则$2×{S_{{2^n}-1}}=n×2+(n-1)×{2^2}+…$+k×2k+1+…+2×2n-1-n-2,
两式相减,得${S_{{2^n}-1}}=-n+2+{2^2}+…+{2^{n-1}}+{2^n}$=2n+1-n-2.
∴S2017=${S}_{{2}^{10}-1}$+S994,
=${S}_{{2}^{10}-1}$+${S}_{{2}^{9}-1}$+S483,
=${S}_{{2}^{10}-1}$+${S}_{{2}^{9}-1}$+${S}_{{2}^{8}-1}$+S228,
=${S}_{{2}^{10}-1}$+${S}_{{2}^{9}-1}$+${S}_{{2}^{8}-1}$+${S}_{{2}^{7}-1}$+S101,
=${S}_{{2}^{10}-1}$+${S}_{{2}^{9}-1}$+${S}_{{2}^{8}-1}$+${S}_{{2}^{7}-1}$+${S}_{{2}^{6}-1}$+S38,
=${S}_{{2}^{10}-1}$+${S}_{{2}^{9}-1}$+${S}_{{2}^{8}-1}$+${S}_{{2}^{7}-1}$+${S}_{{2}^{6}-1}$+${S}_{{2}^{5}-1}$+S7,
=(211-12)+(210-11)+(29-10)+(28-9)+(27-8)+(26-7)+(24-5)
=3986
点评 本题考查新定义的应用,以及等比数列的通项公式公式和求和公式,以及错位相减法,考查了学生的运算能力和转化能力,属于难题.

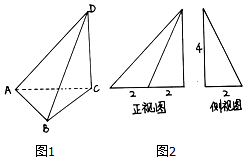 三棱锥D-ABC及其正视图和侧视图如右图所示,且顶点A,B,C,D均在球O的表面上,则球O的表面积为( )
三棱锥D-ABC及其正视图和侧视图如右图所示,且顶点A,B,C,D均在球O的表面上,则球O的表面积为( )| A. | 32π | B. | 36π | C. | 128π | D. | 144π |
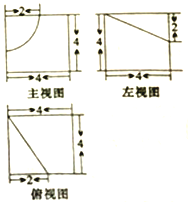
| A. | 64 | B. | 64-4π | C. | 64-8π | D. | 64-$\frac{4π}{3}$ |
| A. | 10 | B. | 9 | C. | 8 | D. | 7 |
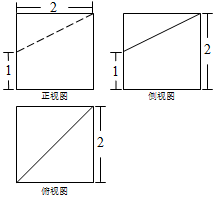
| A. | $\frac{22}{3}$ | B. | $\frac{20}{3}$ | C. | $\frac{16}{3}$ | D. | 6 |
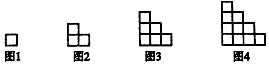 如图图形由小正方形组成,请观察图1至图4的规律,并依此规律,写出第15个图形中小正方形的个数是120.
如图图形由小正方形组成,请观察图1至图4的规律,并依此规律,写出第15个图形中小正方形的个数是120.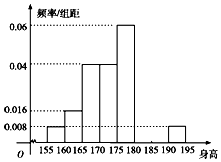 从某学校的1600名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],如图是按上述分组方法得到的频率分布直方图的一部分,第六组的人数为4人.
从某学校的1600名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],如图是按上述分组方法得到的频率分布直方图的一部分,第六组的人数为4人.