题目内容
18.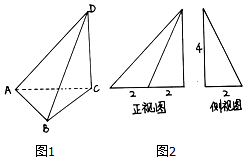 三棱锥D-ABC及其正视图和侧视图如右图所示,且顶点A,B,C,D均在球O的表面上,则球O的表面积为( )
三棱锥D-ABC及其正视图和侧视图如右图所示,且顶点A,B,C,D均在球O的表面上,则球O的表面积为( )| A. | 32π | B. | 36π | C. | 128π | D. | 144π |
分析 由三视图画出几何体的直观图,由三视图判断出DC⊥平面ABC、△ABC的形状,取AC中点F并连BF,由线面垂直的定义和勾股定理求出BC,求出△ABC的外接圆的半径,列出方程求出三棱锥外接球的半径,由球的表面积公式求出答案.
解答 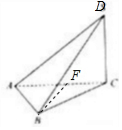 解:由三视图可得:DC⊥平面ABC且底面△ABC为正三角形,
解:由三视图可得:DC⊥平面ABC且底面△ABC为正三角形,
如图所示,取AC中点F,连BF,则BF⊥AC,
在Rt△BCF中,BF=2,CF=2,BC=4,
在Rt△BCD中,CD=4,所以BD=4$\sqrt{2}$.
设球心到平面ABC的距离为d,
因为DC⊥平面ABC,且底面△ABC为正三角形,所以d=2,
因为△ABC的外接圆的半径为2,
所以由勾股定理可得R2=d2+22=8,
则该三棱锥外接球的半径R=2$\sqrt{2}$,
所以三棱锥外接球的表面积是4πR2=32π,
故选A.
点评 本题考查几何体的三视图,线面垂直的定义,以及几何体外接球问题,由三视图正确还原几何体、以及判断几何体位置关系是解题关键.

练习册系列答案
 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
8.现有7名数理化成绩优秀者,分别用A1,A2,A3,B1,B2,C1,C2表示,其中A1,A2,A3的数学成绩优秀,B1,B2的物理成绩优秀,C1,C2的化学成绩优秀.从中选出数学、物理、化学成绩优秀者各1名,组成一个小组代表学校参加竞赛,则A1或B1仅一人被选中的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{6}$ |
10.在等差数列{an}中,a2=2,a6=10,则a10=( )
| A. | 18 | B. | 16 | C. | 14 | D. | 12 |
7.要得到函数$y=cos(\frac{x}{2}-\frac{π}{3})$的图象,只需将函数$y=cos\frac{x}{2}$的图象( )
| A. | 向左平移$\frac{π}{3}$个单位 | B. | 向右平移$\frac{π}{3}$个单位 | ||
| C. | 向左平移$\frac{2π}{3}$个单位 | D. | 向右平移$\frac{2π}{3}$个单位 |
8.函数y=cosx图象上任意一点处的切线倾斜角为α,则α取值范围为( )
| A. | (0,π) | B. | [0,$\frac{π}{4}$] | C. | [0,$\frac{π}{4}$]∪[$\frac{3π}{4}$,π) | D. | [0,$\frac{π}{4}$]∪($\frac{π}{2}$,$\frac{3π}{4}$] |