题目内容

13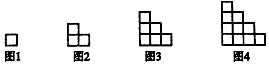．如图图形由小正方形组成，请观察图1至图4的规律，并依此规律，写出第15个图形中小正方形的个数是120．

分析 由a2-a1=2，a3-a2=3，a4-a3=4，可推测an-an-1=n，以上式子累加，结合等差数列的求和公式可得答案．

解答 解：a1=1，a2=3，a3=6，a4=10，
所以a2-a1=2，a3-a2=3，a4-a3=4，…，an-an-1=n，
等式两边同时累加得an-a1=2+3+…+n，
即an=1+2+…+n=$\frac{1}{2}$n（n+1），
所以第15个图形中小正方形的个数是120．
故答案为：120．

点评 本题考查归纳推理，由数列的前几项得出an-an-1=n是解决问题的关键，属基础题．

练习册系列答案
相关题目
13．等差数列{an}的各项均为正数，a1=1，前n项和为Sn；数列{bn}为等比数列，b1=1，且b2S2=6，b2+S3=8．
（1）求数列{an}与{bn}的通项公式；
（2）求{an•bn}的前n项和Tn．
4．在△ABC中，角A，B，C所对的边分别为a，b，c，且b=8，$c=8\sqrt{3}$，S△ABC=16$\sqrt{3}$，那么角A的值为$\frac{π}{6}$或$\frac{5}{6}π$．
1．（$\sqrt{x}$-$\frac{2}{x}$）8的展开式中，x的系数为（　　）
A．-112B．112C．56D．-56
8．现有7名数理化成绩优秀者，分别用A1，A2，A3，B1，B2，C1，C2表示，其中A1，A2，A3的数学成绩优秀，B1，B2的物理成绩优秀，C1，C2的化学成绩优秀．从中选出数学、物理、化学成绩优秀者各1名，组成一个小组代表学校参加竞赛，则A1或B1仅一人被选中的概率为（　　）
A．$\frac{1}{3}$B．$\frac{2}{5}$C．$\frac{1}{2}$D．$\frac{5}{6}$
18．对于定义在R上的函数f（x），若存在正常数a、b，使得f（x+a）≤f（x）+b对一切x∈R均成立，则称f（x）是“控制增长函数”，在以下四个函数中：①f（x）=x2+x+1； ②f（x）=$\sqrt{|x|}$； ③f（x）=sin（x2）；④f（x）=x•sinx．是“控制增长函数”的有（　　）
A．②③B．③④C．②③④D．①②④
5．如果复数$\frac{3-bi}{2+i}（b∈R）$的实部与虚部相等，则b的值为（　　）
A．1B．-6C．3D．-9
2．已知a＞0，函数f（x）=lnx-ax2．
（1）求f（x）的单调区间；
（2）当$a=\frac{1}{8}$时，证明：存在x0∈（2，+∞），使$f（{x_0}）=f（{\frac{3}{2}}）$；
（3）若存在属于区间[1，3]的α，β，且β-α≥1，使f（α）=f（β），证明：$\frac{ln3-ln2}{5}≤a≤\frac{ln2}{3}$．
3．现有正整数构成的数表如下：
第一行：1
第二行：12
第三行：1123
第四行：11211234
第五行：1121123112112345
…
第k行：先抄写第1行，接着按原序抄写第2行，然后按原序抄写第3行，…，直至按原序抄写第k-1行，最后添上数k．（如第四行，先抄写第一行的数1，接着按原序抄写第二行的数1，2，接着按原序抄写第三行的数1，1，2，3，最后添上数4）．
将按照上述方式写下的第n个数记作an（如a1=1，a2=1，a3=2，a4=1，…，a7=3，…，a14=3，a15=4，…）
（1）用tk表示数表第k行的数的个数，求数列{tk}的前k项和Tk；
（2）第8行中的数是否超过73个？若是，用${a_{n_0}}$表示第8行中的第73个数，试求n0和${a_{n_0}}$的值；若不是，请说明理由；
（3）令Sn=a1+a2+a3+…+an，求S2017的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网