题目内容
12．一个几何体的三视图如图所示，则该几何体的体积为（ ）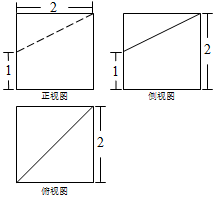
| A． | $\frac{22}{3}$ | B． | $\frac{20}{3}$ | C． | $\frac{16}{3}$ | D． | 6 |
分析 由已知中的三视图可得：该几何体是一个正方体切去一个三棱锥所得的组合体，进而得到答案．
解答 解：由已知中的三视图可得：该几何体是一个正方体切去一个三棱锥所得的组合体，
正方体的体积为：8，
三棱锥的体积为：$\frac{1}{3}$×$\frac{1}{2}$×2×2×1=$\frac{2}{3}$，
故组合体的体积V=8-$\frac{2}{3}$=$\frac{22}{3}$，
故选：A．
点评 本题考查的知识点是棱锥的体积与表面积，棱柱的体积与表面积，简单几何体的三视图，难度中档．
练习册系列答案
相关题目
7．要得到函数$y=cos（\frac{x}{2}-\frac{π}{3}）$的图象，只需将函数$y=cos\frac{x}{2}$的图象（ ）
| A． | 向左平移$\frac{π}{3}$个单位 | B． | 向右平移$\frac{π}{3}$个单位 | ||
| C． | 向左平移$\frac{2π}{3}$个单位 | D． | 向右平移$\frac{2π}{3}$个单位 |
17．
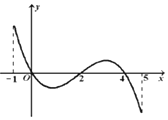已知函数f（x）的定义域为[-1，5]，部分对应值如表，
f（x）的导函数y=f′（x）的图象（该图象关于（2，0）中心对称） 如图所示．
下列关于f（x）的命题：
①函数f（x）的极大值点为 0与4；
②函数f（x）在[0，2]上是减函数；
③函数y=f（x）-a零点的个数可能为0、1、2、3、4个；
④如果当时x∈[-1，t]，f（x）的最大值是2，那么t的最大值为5；．
⑤函数f（x）的图象在[2，4]是上凸的
其中一定正确命题的序号是①②④．
已知函数f（x）的定义域为[-1，5]，部分对应值如表，| x | -1 | 0 | 4 |
| f（x） | 1 | 2 | 2 |
下列关于f（x）的命题：
①函数f（x）的极大值点为 0与4；
②函数f（x）在[0，2]上是减函数；
③函数y=f（x）-a零点的个数可能为0、1、2、3、4个；
④如果当时x∈[-1，t]，f（x）的最大值是2，那么t的最大值为5；．
⑤函数f（x）的图象在[2，4]是上凸的
其中一定正确命题的序号是①②④．
4．一个几何体的三视图如图所示，该几何体的体积为（ ）
| A． | 24-π | B． | 24-3π | C． | $8-\frac{4π}{3}$ | D． | $8-\frac{8π}{3}$ |
1．在△ABC中，$a=2，b=4，C={30°}，则\overrightarrow{BC}•\overrightarrow{CA}$=（ ）
| A． | $4\sqrt{3}$ | B． | 4 | C． | -4$\sqrt{3}$ | D． | -4 |
2．给出如下“三段论”的推理过程：
因为对数函数y=logax（a＞0且a≠1）是增函数，…大前提
而y=${log}_{\frac{1}{2}}x$是对数函数，…小前提
所以y=${log}_{\frac{1}{2}}x$是增函数，…结论
则下列说法正确的是（ ）
因为对数函数y=logax（a＞0且a≠1）是增函数，…大前提
而y=${log}_{\frac{1}{2}}x$是对数函数，…小前提
所以y=${log}_{\frac{1}{2}}x$是增函数，…结论
则下列说法正确的是（ ）
| A． | 推理形式错误 | B． | 大前提错误 | ||
| C． | 小前提错误 | D． | 大前提和小前提都错误 |