题目内容
8．某几何体的三视图如图所示，则该几何体的体积为（ ）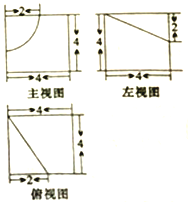
| A． | 64 | B． | 64-4π | C． | 64-8π | D． | 64-$\frac{4π}{3}$ |
分析 由三视图可知：该几何体是一个正方体去掉一个圆锥的$\frac{1}{4}$．
解答 解：由三视图可知：该几何体是一个正方体去掉一个圆锥的$\frac{1}{4}$．
∴该几何体的体积=43-$\frac{1}{4}×\frac{1}{3}×π×{2}^{2}×4$=64-$\frac{4π}{3}$．
故选：D．
点评 本题考查了正方体与球的三视图、体积计算公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
18．对于定义在R上的函数f（x），若存在正常数a、b，使得f（x+a）≤f（x）+b对一切x∈R均成立，则称f（x）是“控制增长函数”，在以下四个函数中：①f（x）=x2+x+1； ②f（x）=$\sqrt{|x|}$； ③f（x）=sin（x2）；④f（x）=x•sinx．是“控制增长函数”的有（ ）
| A． | ②③ | B． | ③④ | C． | ②③④ | D． | ①②④ |
13．在△ABC中，已知三个内角为A，B，C满足sinA：sinB：sinC=6：5：4，则sinB=（ ）
| A． | $\frac{{\sqrt{7}}}{4}$ | B． | $\frac{3}{4}$ | C． | $\frac{{5\sqrt{7}}}{16}$ | D． | $\frac{9}{16}$ |
17．
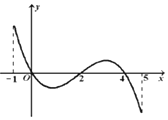已知函数f（x）的定义域为[-1，5]，部分对应值如表，
f（x）的导函数y=f′（x）的图象（该图象关于（2，0）中心对称） 如图所示．
下列关于f（x）的命题：
①函数f（x）的极大值点为 0与4；
②函数f（x）在[0，2]上是减函数；
③函数y=f（x）-a零点的个数可能为0、1、2、3、4个；
④如果当时x∈[-1，t]，f（x）的最大值是2，那么t的最大值为5；．
⑤函数f（x）的图象在[2，4]是上凸的
其中一定正确命题的序号是①②④．
已知函数f（x）的定义域为[-1，5]，部分对应值如表，| x | -1 | 0 | 4 |
| f（x） | 1 | 2 | 2 |
下列关于f（x）的命题：
①函数f（x）的极大值点为 0与4；
②函数f（x）在[0，2]上是减函数；
③函数y=f（x）-a零点的个数可能为0、1、2、3、4个；
④如果当时x∈[-1，t]，f（x）的最大值是2，那么t的最大值为5；．
⑤函数f（x）的图象在[2，4]是上凸的
其中一定正确命题的序号是①②④．
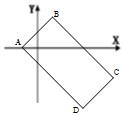如图，已知复平面内平行四边形ABCD中，点A对应的复数为-1，$\overrightarrow{AB}$对应的复数为2+2i，$\overrightarrow{BC}$对应的复数为4-4i．