题目内容
14.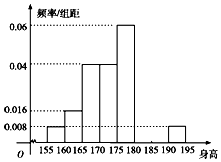 从某学校的1600名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],如图是按上述分组方法得到的频率分布直方图的一部分,第六组的人数为4人.
从某学校的1600名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],如图是按上述分组方法得到的频率分布直方图的一部分,第六组的人数为4人.(1)求第七组的频率;
(2)估计该校1600名男生中身高在180cm以上(含180cm)的人数;
(3)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,设他们的身高分别为x,y,记事件E={(x,y)||x-y|≤5},求事件E的概率.
分析 (1)先求出第六组的频率,由此利用频率分布直方图能求出第七组的频率.
(2)由频率分布直方图求出后三组频率,由此能估计该校1600名男生中身高在180 cm以上(含180 cm)的人数.
(3)第六组[180,185)的人数为4人,设为a,b,c,d,第八组[190,195]的人数为2人,设为A,B,由此利用列举法能求出事件E的概率.
解答 解:(1)第六组的频率为$\frac{4}{50}$=0.08.
所以第七组的频率为:
1-0.08-5×(0.008×2+0.016+0.04×2+0.06)=0.06.
(2)由直方图得后三组频率为0.06+0.08+0.008×5=0.18,
所以估计该校1600名男生中身高在180 cm以上(含180 cm)的人数为0.18×1600=288人.
(3)第六组[180,185)的人数为4人,设为a,b,c,d,
第八组[190,195]的人数为2人,设为A,B,
则有ab,ac,ad,bc,bd,cd,aA,bA,cA,dA,aB,bB,cB,dB,AB,共15种情况.
因为事件E={(x,y)||x-y|≤5}发生当且仅当随机抽取的两名男生在同一组,
所以事件E包含的基本事件为ab,ac,ad,bc,bd,cd,AB共7种情况,
故P(E)=$\frac{7}{15}$.
点评 本题考查频率分布直方图的应用,考查概率的求法,考查数据处理能力、运算求解能力,考查数形结合思想、化归与转化思想、集合思想,是基础题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
5.如果复数$\frac{3-bi}{2+i}(b∈R)$的实部与虚部相等,则b的值为( )
| A. | 1 | B. | -6 | C. | 3 | D. | -9 |
4.一个几何体的三视图如图所示,该几何体的体积为( )


| A. | 24-π | B. | 24-3π | C. | $8-\frac{4π}{3}$ | D. | $8-\frac{8π}{3}$ |