题目内容

下列函数中，最小正周期为π的偶函数是（　　）
A、y=sin2x
B、y=cos
x
2
C、y=sin2x+cos2x
D、y=
1-tan2x
1+tan2x
考点：三角函数的周期性及其求法,三角函数中的恒等变换应用
专题：三角函数的图像与性质
分析：利用三角函数的周期性及奇偶性对A、B、C、D四个选项逐一判断即可．
解答： 解：A，y=sin2x为奇函数，故排除A；
B，y=cos
x
2
的周期T=
2π
1
2
=4π≠π，可排除B；
C，y=f（x）=sin2x+cos2x，f（-x）=sin2（-x）+cos2（-x）=-sin2x+cos2x≠f（x），该函数非偶，排除C；
D，y=f（x）=
1-tan2x
1+tan2x
=cos2x（x≠kπ+
π
2
，k∈Z），其周期T=
2π
2
=π，满足f（-x）=f（x），为偶函数，故D正确；
故选：D．
点评：本题考查三角函数的周期性及奇偶性，考查二倍角的余弦与三角恒等变换，属于中档题．
练习册系列答案
相关题目
若f（x）=x2-ax+b，f（1）=-1，f（2）=2，则f（-4）=
 
．
在直角坐标系和以原点为极点，以x轴正方向为极轴建立的极坐标系中，直线l：y+kx+2=0与曲线C：ρ=2cosθ相交，则k的取值范围是（　　）
A、k∈R
B、k≥-
3
4
C、k＜-
3
4
D、k∈R但k≠0
已知AB，BC，CD为两两垂直的三条线段，且它们的长都等于1，则AD的长为（　　）
A、1
B、2
C、3
D、
3
已知空间图形的三视图如图，空间几何体的表面积为（　　）
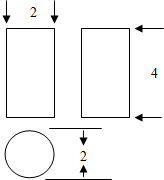
A、8πB、10π
C、12πD、9π
对于任意实数x，符号[x]表示“不超过x的最大整数”，如[-2]=-2，[1.3]=1，[-2.5]=-3，定义函数f（x）=sin（
π
2
[x]）．给出下列四个命题：
①函数y=f（x）是奇函数；
②函数y=f（x）的值域是[-1，1]；
③函数y=f（x）是周期函数，且最小正周期为4；
④函数y=f（x）的图象与直线y=x-1有三个不同的公共点．
其中真命题的个数为（　　）
A、1个B、2个C、3个D、4个
数列{an}的通项公式是an=
1
n
+
n+1
，前n项和为9，则n等于（　　）
A、9B、99C、10D、100
已知函数f（x）=（ax+1）ex
（Ⅰ）若a=-1，求函数f（x）的单调区间；
（Ⅱ）当a＞0时，求函数f（x）在[-2，0]的最小值；
（Ⅲ）设n∈N，a=0，F（x）=f（x）-x，求证：
(n+1)(n+2)
2
＜
en+1
e-1
．
已知
a
=（1，1），
b
=（-2，2），
c
=（2，k）．
（1）若（
a
-
b
）∥
c
，求k的值．
（2）若
a
⊥
c
，求k的值．
（3）若
a
与 
c
的夹角为锐角，求k的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网