题目内容
14.已知函数f(x)=lnx-mx(m∈R),g(x)=2f(x)+x2,h(x)=lnx-cx2-bx.(1)求函数f(x)的单调区间;
(2)当$m≥\frac{{3\sqrt{2}}}{2}$时,g(x)的两个极值点为x1,x2(x1<x2).
①证明:$0<\frac{x_1}{x_2}≤\frac{1}{2}$;
②若x1,x2恰为h(x)的零点,求$y=({x_1}-{x_2})h'(\frac{{{x_1}+{x_2}}}{2})$的最小值.
分析 (1)求出函数的导数,通过讨论m的范围,求出函数的单调区间即可;
(2)①求出函数的导数,令$\frac{x_1}{x_2}=t$(0<t<1),得$t+\frac{1}{t}+2={m^2}$,从而证出结论;
②根据$ln{x_1}-c{x_1}^2-b{x_1}=0$,$ln{x_2}-c{x_2}^2-b{x_2}=0$,两式相减得$ln\frac{x_1}{x_2}-c({x_1}-{x_2})({x_1}+{x_2})-b({x_1}-{x_2})=0$,令$\frac{x_1}{x_2}=t$($0<t≤\frac{1}{2}$),$G(t)=2•\frac{t-1}{t+1}-lnt$,根据函数的单调性求出函数的最小值即可.
解答 解:(1)∵函数f(x)=lnx-mx,∴$f'(x)=\frac{1}{x}-m=\frac{1-mx}{x}$,x>0;
当m>0时,由1-mx>0解得$x<\frac{1}{m}$,即当$0<x<\frac{1}{m}$时,f'(x)>0,f(x)单调递增;
由1-mx<0解得$x>\frac{1}{m}$,即当$x>\frac{1}{m}$时,f'(x)<0,f(x)单调递减;
当m≤0时,1-mx>0,故f'(x)>0,即f(x)在(0,+∞)上单调递增;
∴当m>0时,f(x)的单调增区间为$(0,\frac{1}{m})$,单调减区间为$(\frac{1}{m},+∞)$;
当m≤0时,f(x)的单调递增区间为(0,+∞).
(2)①g(x)=2f(x)+x2=2lnx-2mx+x2,则$g'(x)=\frac{{2({x^2}-mx+1)}}{x}$,
∴g'(x)的两根x1,x2即为方程x2-mx+1=0的两根;
又∵$m≥\frac{{3\sqrt{2}}}{2}$,∴△=m2-4>0,x1+x2=m,x1x2=1
令$\frac{x_1}{x_2}=t$(0<t<1),由${({x_1}+{x_2})^2}={m^2}$,得${x_1}^2+{x_2}^2+2{x_1}{x_2}={m^2}$,
因为x1x2=1,两边同时除以x1x2,得$t+\frac{1}{t}+2={m^2}$,且$m≥\frac{{3\sqrt{2}}}{2}$,
故$t+\frac{1}{t}≥\frac{5}{2}$,解得$t≤\frac{1}{2}$或t≥2,∴$0<t≤\frac{1}{2}$,即$0<\frac{x_1}{x_2}≤\frac{1}{2}$.
②∵x1,x2为h(x)=lnx-cx2-bx的零点,
∴$ln{x_1}-c{x_1}^2-b{x_1}=0$,$ln{x_2}-c{x_2}^2-b{x_2}=0$,
两式相减得$ln\frac{x_1}{x_2}-c({x_1}-{x_2})({x_1}+{x_2})-b({x_1}-{x_2})=0$,
∵$h'(x)=\frac{1}{x}-2cx-b$,
∴$y=({x_1}-{x_2})[{\frac{2}{{{x_1}+{x_2}}}-c({x_1}+{x_2})-b}]$=$\frac{{2({x_1}-{x_2})}}{{{x_1}+{x_2}}}-ln\frac{x_1}{x_2}=2•\frac{{\frac{x_1}{x_2}-1}}{{\frac{x_1}{x_2}+1}}-ln\frac{x_1}{x_2}$,
令$\frac{x_1}{x_2}=t$($0<t≤\frac{1}{2}$),$G(t)=2•\frac{t-1}{t+1}-lnt$,
则$G'(t)=\frac{{-{{(t-1)}^2}}}{t(t+1)}<0$,y=G(t)在$(0,\frac{1}{2}]$上是减函数,
∴$G{(t)_{min}}=G(\frac{1}{2})=-\frac{2}{3}+ln2$,
即$y=({x_1}-{x_2})h'(\frac{{{x_1}+{x_2}}}{2})$的最小值为$-\frac{2}{3}+ln2$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想、转化思想,是一道综合题.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | $\frac{\sqrt{6}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{15}}{3}$ | D. | $\sqrt{3}$ |
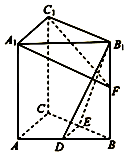 如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱BB1上,且B1D⊥A1F,A1C1⊥A1B1.
如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱BB1上,且B1D⊥A1F,A1C1⊥A1B1.