题目内容
6.复数z满足z(2+i)=3-i,则复数z在复平面内对应的点位于( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 由z(2+i)=3-i,得$z=\frac{3-i}{2+i}$,再利用复数代数形式的乘除运算化简复数z,求出复数z在复平面内对应的点的坐标,则答案可求.
解答 解:由z(2+i)=3-i,
得$z=\frac{3-i}{2+i}$=$\frac{(3-i)(2-i)}{(2+i)(2-i)}=\frac{5-5i}{5}=1-i$,
则复数z在复平面内对应的点的坐标为:(1,-1),位于第四象限.
故选:D.
点评 本题考查了复数代数形式的乘除运算,考查了复数的代数表示法及其几何意义,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.如图所示的程序框图,输出的值为( )
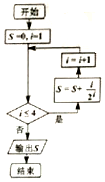

| A. | $\frac{15}{16}$ | B. | $\frac{15}{12}$ | C. | $\frac{13}{8}$ | D. | $\frac{13}{4}$ |
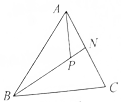 如图,在△ABC中,已知$\overrightarrow{AN}$=$\frac{1}{2}\overrightarrow{AC}$,P是BN上一点,若$\overrightarrow{AP}=m\overrightarrow{AB}+\frac{1}{4}\overrightarrow{AC}$,则实数m的值是$\frac{1}{2}$.
如图,在△ABC中,已知$\overrightarrow{AN}$=$\frac{1}{2}\overrightarrow{AC}$,P是BN上一点,若$\overrightarrow{AP}=m\overrightarrow{AB}+\frac{1}{4}\overrightarrow{AC}$,则实数m的值是$\frac{1}{2}$.