题目内容
9.已知圆O:x2+y2=4与y轴正半轴的交点为M,点M沿圆O顺时针运动$\frac{π}{2}$弧长到达点N,以x轴的非负半轴为始边,ON为终边的角记为α,则tanα=1.分析 根据题意画出图象,再结合题意求出点M旋转的角对应的弧度数度,再求出角α,再求正切值.
解答 解:由题意得,M(0,2),并画出图象如下:
∵点M沿圆O顺时针运动$\frac{π}{2}$弧长到达点N,
∴旋转的角的弧度数为$\frac{\frac{π}{2}}{2}$=$\frac{π}{4}$,
即以ON为终边的角α=$\frac{π}{4}$,则tanα=1,
故答案为1.
点评 本题考查任意角的三角函数的定义,以及弧度制的定义,关键是根据题意正确画图,求出旋转的角度.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
4.x>1是“x>2”的( )
| A. | 充要条件 | B. | 必要条件 | ||
| C. | 必要非充分条件 | D. | 既非充分又非必要条件 |
19.随着社会的发展,终身学习成为必要,工人知识要更新,学习培训必不可少,现某工厂有工人1000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人),从该工厂的工人中共抽查了100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数)得到A类工人生产能力的茎叶图(图1),B类工人生产能力的频率分布直方图(图2).
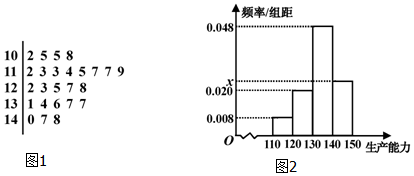
(Ⅰ)问A类、B类工人各抽查了多少工人,并求出直方图中的x;
(Ⅱ)求A类工人生产能力的中位数,并估计B类工人生产能力的平均数(同一组中的数据用该组区间的中点值作代表);
(Ⅲ) 若规定生产能力在[130,150]内为能力优秀,由以上统计数据在答题卡上完成下面的2×2列联表,并判断是否可以在犯错误概率不超过0.1%的前提下,认为生产能力与培训时间长短有关.
能力与培训时间列联表
参考数据:
参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.

(Ⅰ)问A类、B类工人各抽查了多少工人,并求出直方图中的x;
(Ⅱ)求A类工人生产能力的中位数,并估计B类工人生产能力的平均数(同一组中的数据用该组区间的中点值作代表);
(Ⅲ) 若规定生产能力在[130,150]内为能力优秀,由以上统计数据在答题卡上完成下面的2×2列联表,并判断是否可以在犯错误概率不超过0.1%的前提下,认为生产能力与培训时间长短有关.
能力与培训时间列联表
| 短期培训 | 长期培训 | 合计 | |
| 能力优秀 | 8 | 54 | 62 |
| 能力不优秀 | 17 | 21 | 38 |
| 合计 | 25 | 75 | 100 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
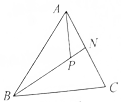 如图,在△ABC中,已知$\overrightarrow{AN}$=$\frac{1}{2}\overrightarrow{AC}$,P是BN上一点,若$\overrightarrow{AP}=m\overrightarrow{AB}+\frac{1}{4}\overrightarrow{AC}$,则实数m的值是$\frac{1}{2}$.
如图,在△ABC中,已知$\overrightarrow{AN}$=$\frac{1}{2}\overrightarrow{AC}$,P是BN上一点,若$\overrightarrow{AP}=m\overrightarrow{AB}+\frac{1}{4}\overrightarrow{AC}$,则实数m的值是$\frac{1}{2}$.