题目内容
四面体ABCD中，AD=BC，且AD⊥BC，E、F分别是AB、CD的中点，则EF与BC所成的角为（ ）
| A、30° | B、45° |
| C、60° | D、90° |
考点：异面直线及其所成的角
专题：空间角
分析：首先作线段的中点，利用三角形的中位线建立线线间的联系，利用平行线把异面面直线问题转化为平面直线问题，进一步利用三角形的性质求得结果．
解答：
解：取AC的中点，连接EF，
则：在四面体ABCD中，E、F分别是AB、CD的中点，
所以：EG∥BC，FG∥AD
由于：AD=BC，且AD⊥BC，
EG=FG=
AD=
BC
所以：△EFG是等腰直角三角形．
所以：EF与BC所成的角为∠GEF=45°
故选：B
则：在四面体ABCD中，E、F分别是AB、CD的中点，
所以：EG∥BC，FG∥AD
由于：AD=BC，且AD⊥BC，
EG=FG=
| 1 |
| 2 |
| 1 |
| 2 |
所以：△EFG是等腰直角三角形．
所以：EF与BC所成的角为∠GEF=45°
故选：B
点评：本题考查的知识要点：异面直线所成的角的应用中位线的性质的应用．属于基础题型．
练习册系列答案
相关题目
设A={1，2，3}，B={x|x⊆A}，则下列关系表述正确的是（ ）
| A、A∈B | B、A∉B |
| C、A?B | D、A⊆B |
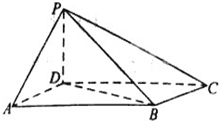如图所示，四棱锥P-ABCD中，底面ABCD为平行四边形，且∠DAB=60°，AB=2AD=2，PD⊥底面ABC，则：（1）证明：PA⊥BD；
（2）若PD=AD，求平面APB与平面CPB夹角的余弦值．
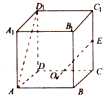如图，在棱长为2的正方体ABCD-A1B1C1D1中，O为底面ABCD的中心，E为CC1的中点，那么异面直线OE与AD1所成角的余弦值等于已知抛物线x2=4y上有一点长为6的弦AB所在直线倾斜角为45°，则AB中点到x轴的距离为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|