题目内容
2.△ABC的三内角A,B,C所对边长分别是a,b,c,设向量$\overrightarrow n=(\sqrt{3}a+c,sinB-sinA)$,$\overrightarrow m=(a+b,sinC)$,若$\overrightarrow m∥\overrightarrow n$,则角B的大小为( )| A. | $\frac{π}{6}$ | B. | $\frac{5π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
分析 由$\overrightarrow m∥\overrightarrow n$,利用数量积运算及其正弦定理、余弦定理即可得出.
解答 解:若$\overrightarrow m∥\overrightarrow n$,
则(a+b)(sinB-sinA)-sinC($\sqrt{3}$a+c)=0,
由正弦定理可得:(a+b)(b-a)-c($\sqrt{3}$a+c)=0,
化为a2+c2-b2=-$\sqrt{3}$ac,
∴cosB=$\frac{{a}^{2}{+c}^{2}{-b}^{2}}{2ac}$=-$\frac{\sqrt{3}}{2}$,
∵B∈(0,π),
∴B=$\frac{5π}{6}$,
故选:B.
点评 本题考查了正弦定理与余弦定理的应用、向量数量积运算性质,考查了推理能力与计算能力,是一道基础题.

练习册系列答案
相关题目
11.已知集合$M=\left\{{x|\frac{3}{x^2}<1}\right\},N=\left\{{n|1≤{2^n}≤13且n∈Z}\right\}$,则N∩M=( )
| A. | {2,3} | B. | {3} | C. | $[{0,\sqrt{3}})$ | D. | [2,+∞) |
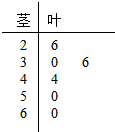 PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国PM2.5标准采用世卫组织设定的最宽限值.即PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米--75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.某市环保局从市区今年9月每天的PM2.5监测数据中,按系统抽样方法抽取了某6天的数据作为样本,其监测值如茎叶图所示.
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国PM2.5标准采用世卫组织设定的最宽限值.即PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米--75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.某市环保局从市区今年9月每天的PM2.5监测数据中,按系统抽样方法抽取了某6天的数据作为样本,其监测值如茎叶图所示.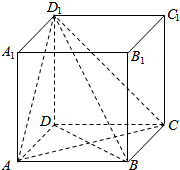 如图,在正方形ABCD-A′B′C′D′,AB=1,
如图,在正方形ABCD-A′B′C′D′,AB=1,