题目内容
3.已知命题p:方程$\frac{{x}^{2}}{t+2}$+$\frac{{y}^{2}}{t-10}$=1表示双曲线,命题q:1-m<t<1+m(m>0). 若q是p的充分非必要条件,试求实数m的取值范围.
分析 q是p的充分条件,利用不等式即可求出实数m的取值范围.
解答 解:由命题p得(t+2)(t-10)<0,即-2<t<10,即t∈(-2,10),
由命题q:1-m<t<1+m(m>0),即t∈(1-m,1+m)
∵q是p的充分非必要条件,
∴(1-m,1+m)?(-2,10),
∴由1-m≥2,1+m≤10(不同时取等号)及m>0得0<m≤3,
∴所求m的取值范围为(0,3].
点评 本题考查了充分必要条件的定义,不等式的求解,属于基础题.

练习册系列答案
相关题目
11.已知集合$M=\left\{{x|\frac{3}{x^2}<1}\right\},N=\left\{{n|1≤{2^n}≤13且n∈Z}\right\}$,则N∩M=( )
| A. | {2,3} | B. | {3} | C. | $[{0,\sqrt{3}})$ | D. | [2,+∞) |
13.若函数f(x)同时满足以下三个性质:①f(x)的最小正周期为π;②对任意的x∈R,都有f(x-$\frac{π}{4}$)+f(-x)=0;③f(x)在($\frac{π}{4}$,$\frac{π}{2}$)上是减函数,则f(x)的解析式可能是( )
| A. | f(x)=sin2x+cos2x | B. | f(x)=sin2x | C. | f(x)=tan(x+$\frac{π}{8}$) | D. | f(x)=cos2x |
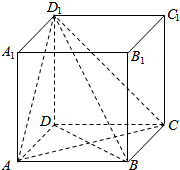 如图,在正方形ABCD-A′B′C′D′,AB=1,
如图,在正方形ABCD-A′B′C′D′,AB=1,