题目内容
17.已知三点P(5,2),F1(-6,0),F2(4,0),以F1,F2为焦点且过点P的椭圆的标准方程是$\frac{(x+1)^{2}}{45}$+$\frac{{y}^{2}}{20}$=1.分析 设所求椭圆方程为$\frac{(x+1)^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),其半焦距c=5.由于点P(5,2)在椭圆上,利用椭圆的定义可得2a=|PF1|+|PF2|,再利用b2=a2-c2即可得出椭圆方程.
解答 解:依题意,椭圆的中心为F1F2的中点(-1,0),
设所求椭圆方程为$\frac{(x+1)^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
其半焦距c=5.
∵点P(5,2)在椭圆上,
∴2a=|PF1|+|PF2|=$\sqrt{(5+6)^{2}+{2}^{2}}$+$\sqrt{(5-4)^{2}+{2}^{2}}$=6$\sqrt{5}$.
∴a=3$\sqrt{5}$,从而b2=a2-c2=20.
故所求椭圆的标准方程是 $\frac{(x+1)^{2}}{45}$+$\frac{{y}^{2}}{20}$=1.
故答案为:$\frac{(x+1)^{2}}{45}$+$\frac{{y}^{2}}{20}$=1.
点评 本题考查椭圆方程的求法,注意运用待定系数法和椭圆的定义,考查运算能力,属于中档题.

练习册系列答案
相关题目
9.在△ABC中,a2+b2-c2=ab,则cosC=( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $-\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
6.函数y=loga(x+1)(a>0且a≠1)的图象恒过点为( )
| A. | (1,0) | B. | (0,1) | C. | (-1,0) | D. | (0,0) |
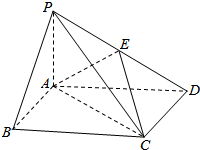 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD中点.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD中点.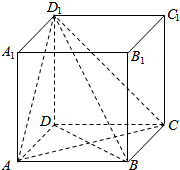 如图,在正方形ABCD-A′B′C′D′,AB=1,
如图,在正方形ABCD-A′B′C′D′,AB=1,