题目内容
7．从甲、乙、丙、丁四名同学中选2人参加普法知识竞赛，则甲被选中的概率为（ ）| A． | $\frac{3}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{2}$ |
分析 先求出基本事件总数n=${C}_{4}^{2}$=6，再求出甲被选中包含听基本事件个数m=${C}_{1}^{1}{C}_{3}^{1}$=3，由此能求出甲被选中的概率．
解答 解：从甲、乙、丙、丁四名同学中选2人参加普法知识竞赛，
基本事件总数n=${C}_{4}^{2}$=6，
甲被选中包含听基本事件个数m=${C}_{1}^{1}{C}_{3}^{1}$=3，
∴甲被选中的概率为p=$\frac{m}{n}=\frac{3}{6}=\frac{1}{2}$．
故选：D．
点评 本题考查概率的求法，是基础题，解题时要认真审题，注意等可能事件概率计算公式的合理运用．
练习册系列答案
学业测评一课一测系列答案
小学课时作业全通练案系列答案
相关题目
17．已知平面向量$\overrightarrow{a}$=（1，-1），$\overrightarrow{b}$=（1，1），则向量$\frac{3}{2}\overrightarrow{a}$-$\frac{1}{2}\overrightarrow{b}$等于（ ）
| A． | （2，1） | B． | （1，-2） | C． | （1，0） | D． | （2，-1） |
18．在等差数列{an}中，若a3=9，a6=15，则a12等于（ ）
| A． | 3 | B． | 12 | C． | 27 | D． | 36 |
15．函数y=cos2x，x∈R的最小正周期为（ ）
| A． | 2 | B． | π | C． | 2π | D． | $\frac{1}{π}$ |
2．直线l1：2x-y-1=0与直线l2：mx+y+1=0互相垂直的充要条件是（ ）
| A． | m=-2 | B． | m=-$\frac{1}{2}$ | C． | m=$\frac{1}{2}$ | D． | m=2 |
12．某次考试，班主任从全班同学中随机抽取一个容量为8的样本，他们的数学、物理分数对应如下表：
绘出散点图如下：
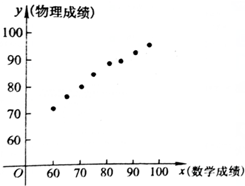
根据以上信息，判断下列结论：
①根据此散点图，可以判断数学成绩与物理成绩具有线性相关关系；
②根据此散点图，可以判断数学成绩与物理成绩具有一次函数关系；
③甲同学数学考了80分，那么，他的物理成绩一定比数学只考了60分的乙同学的物理成绩要高．
其中正确的个数为（ ）
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学分数x | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
| 物理分数y | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
根据以上信息，判断下列结论：
①根据此散点图，可以判断数学成绩与物理成绩具有线性相关关系；
②根据此散点图，可以判断数学成绩与物理成绩具有一次函数关系；
③甲同学数学考了80分，那么，他的物理成绩一定比数学只考了60分的乙同学的物理成绩要高．
其中正确的个数为（ ）
| A． | 0 | B． | 3 | C． | 2 | D． | 1 |
19．已知向量$\overrightarrow{a}$=（5，2），$\overrightarrow{b}$=（1，6），则$\overrightarrow{a}$+$\overrightarrow{b}$的坐标为（ ）
| A． | （4，-4） | B． | （6，8） | C． | （5，12） | D． | （3，11） |
16．已知函数f（x）=x3-x+3，则曲线y=f（x）在点（1，f（1））处的切线方程为（ ）
| A． | 2x-y+1=0 | B． | x-2y+1=0 | C． | 2x+y+1=0 | D． | 2x-y+2=0 |
19．函数f（x）=$\frac{1}{{\sqrt{x-2}}}$的定义域为（ ）
| A． | （-∞，2）∪（2，+∞） | B． | （2，+∞） | C． | [2，+∞） | D． | （-∞，2） |