题目内容

17．已知平面向量$\overrightarrow{a}$=（1，-1），$\overrightarrow{b}$=（1，1），则向量$\frac{3}{2}\overrightarrow{a}$-$\frac{1}{2}\overrightarrow{b}$等于（　　）
A．（2，1）B．（1，-2）C．（1，0）D．（2，-1）

分析 由平面向量$\overrightarrow{a}$=（1，-1），$\overrightarrow{b}$=（1，1），利用向量的坐标运算法则能求出向量$\frac{3}{2}\overrightarrow{a}$-$\frac{1}{2}\overrightarrow{b}$．

解答 解：∵平面向量$\overrightarrow{a}$=（1，-1），$\overrightarrow{b}$=（1，1），
∴向量$\frac{3}{2}\overrightarrow{a}$-$\frac{1}{2}\overrightarrow{b}$=（$\frac{3}{2}，-\frac{3}{2}$）-（$\frac{1}{2}，\frac{1}{2}$）=（1，-2）．
故选：B．

点评 本题考查平面向量坐标求法，是基础题，解题时要认真审题，注意向量的坐标运算法则的合理运用．

练习册系列答案
相关题目
7．设m，n∈N，f（x）=（1+x）m+（1+x）n．
（1）当m=n=5时，若$f（x）={a_5}{（1-x）^5}+{a_4}{（1-x）^4}+…+{a_1}（1-x）+{a_0}$，求a0+a2+a4的值；
（2）f（x）展开式中x的系数是9，当m，n变化时，求x2系数的最小值．
8．如图所示，程序据图（算法流程图）的输出结果为（　　）
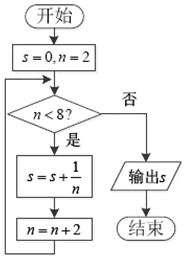
A．$\frac{3}{4}$B．$\frac{1}{6}$C．$\frac{11}{12}$D．$\frac{25}{24}$
5．f（x）为奇函数，且x＞0时，f（x）=x2-2x，则x＜0时，f（x）=（　　）
A．f（x）=x2+2-xB．f（x）=x2-2-xC．f（x）=-x2+2-xD．f（x）=-x2-2-x
12．已知函数$f（x）=\frac{x}{{1+{x^2}}}$，x∈（0，1）．
（1）令x1，x2∈（0，1），证明：（x1-x2）•[f（x1）-f（x2）]≥0；
（2）若x∈（0，1）时，恒有$\frac{{3{x^2}-x}}{{1+{x^2}}}≥a（{x-\frac{1}{3}}）$，求a的值；
（3）若x1，x2，x3都是正数，且x1+x2+x3=1，求$y=\frac{{3x_1^2-{x_1}}}{1+x_1^2}+\frac{{3x_2^2-{x_2}}}{1+x_2^2}+\frac{{3x_3^2-{x_3}}}{1+x_3^2}$的最小值．
2．抛物线y2=8x的准线方程是（　　）
A．x=2B．y=2C．x=-2D．y=-2
9．在区间[-2，3]上随机取一个数x，则x∈[-1，1]的概率是（　　）
A．$\frac{1}{5}$B．$\frac{2}{5}$C．$\frac{1}{2}$D．$\frac{3}{5}$
6．设变量x，y满足约束条件$\left\{\begin{array}{l}{x-y+1≥0}\\{x+y≥0}\\{x≤0}\end{array}\right.$，则z=x+2y的最小值为（　　）
A．0B．0.5C．2D．9
7．从甲、乙、丙、丁四名同学中选2人参加普法知识竞赛，则甲被选中的概率为（　　）
A．$\frac{3}{4}$B．$\frac{1}{3}$C．$\frac{1}{4}$D．$\frac{1}{2}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网