题目内容
函数f（x）=
的值域为 ．
| 1-ex |
考点：函数的值域
专题：函数的性质及应用
分析：根据指数函数的单调性的性质，结合根式的性质即可求出函数的值域．
解答：
解：∵ex＞0，
∴-ex＜0，
则0≤1-ex＜1，
则0≤
＜1，
即0≤f（x）＜1，
故函数的值域为[0，1），
故答案为：[0，1）
∴-ex＜0，
则0≤1-ex＜1，
则0≤
| 1-ex |
即0≤f（x）＜1，
故函数的值域为[0，1），
故答案为：[0，1）
点评：本题主要考查函数值域的求解，根据指数的单调性的性质是解决本题的关键．
练习册系列答案
相关题目
已知底面边长为1，高为2的正六棱柱的顶点都在一个球面上，则该球的表面积为（ ）
| A、4π | ||||
| B、8π | ||||
C、
| ||||
D、
|
已知AE是△ABC的中线，若∠A=120°，
•
=-2，则|
|的最小值是（ ）
| AC |
| AB |
| AE |
| A、-1 | B、0 | C、1 | D、2 |
“ab＞0且a+b＜0”是“a与b均为负数的”（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
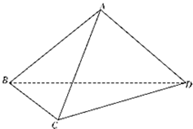A是△BCD所在平面外的点，∠BAC=∠CAD=∠DAB=60°，AB=3，AC=AD=2．