题目内容
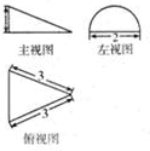
某几何体的三视图是如图所示,其中左视图为半圆,则该几何体的体积是( )

A、
| ||||
B、
| ||||
C、
| ||||
| D、π |
考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:根据几何体的三视图,得出该几何体是平放的半圆锥,结和数据求出它的体积即可.
解答:
解:根据几何体的三视图,得;
该几何体是平放的半圆锥,且圆锥的底面半径为1,母线长为3,
∴圆锥的高为
=2
;
∴该几何体的体积为
V半圆锥=
×
π×12×2
=
π.
故选:A.
该几何体是平放的半圆锥,且圆锥的底面半径为1,母线长为3,
∴圆锥的高为
| 32-12 |
| 2 |
∴该几何体的体积为
V半圆锥=
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| ||
| 3 |
故选:A.
点评:本题考查了利用空间几何体的三视图的求体积的应用问题,是基础题目.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
如果复数
(其中i为虚数单位,b为实数)的实部和虚部互为相反数,那么b等于( )
| 2-bi |
| 1+2i |
| A、-6 | ||
B、
| ||
C、-
| ||
| D、2 |
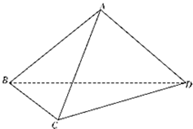 A是△BCD所在平面外的点,∠BAC=∠CAD=∠DAB=60°,AB=3,AC=AD=2.
A是△BCD所在平面外的点,∠BAC=∠CAD=∠DAB=60°,AB=3,AC=AD=2.