题目内容
椭圆
+
=1(a>b>0)上任意一点到两焦点的距离分别为d1,d2,焦距为2c,若d1,2c,d2成等差数列,则椭圆的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由题设条件,结合椭圆的定义知:d1+d2=2a,由d1,2c,d2成等差数列,得到d1+d2=4c,由此能求出椭圆的离心率.
解答:
解:∵椭圆
+
=1(a>b>0)上任意一点到两焦点的距离分别为d1,d2,
∴由椭圆的定义知:d1+d2=2a,
∵焦距为2c,且d1,2c,d2成等差数列,
∴d1+d2=4c,
∴2a=4c,即a=2c,
∴e=
=
.
故选:A.
| x2 |
| a2 |
| y2 |
| b2 |
∴由椭圆的定义知:d1+d2=2a,
∵焦距为2c,且d1,2c,d2成等差数列,
∴d1+d2=4c,
∴2a=4c,即a=2c,
∴e=
| c |
| a |
| 1 |
| 2 |
故选:A.
点评:本题考查椭圆的离心率的求法,解题时要注意椭圆定义和等差数列的性质的灵活运用,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
Sn是等差数列{an}的前n项和,若S5=20,则a3=( )
| A、5 | B、6 | C、9 | D、4 |
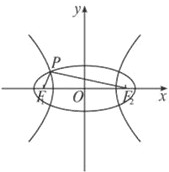 如图,F1,F2是椭圆C1与双曲线C2的公共焦点,点P是椭圆和双曲线的一个交点,并且PF1⊥PF2,e1,e2分别是椭圆和双曲线的离心率,则( )
如图,F1,F2是椭圆C1与双曲线C2的公共焦点,点P是椭圆和双曲线的一个交点,并且PF1⊥PF2,e1,e2分别是椭圆和双曲线的离心率,则( )| A、e1e2≥2 | ||||
| B、e12+e22≥4 | ||||
C、
| ||||
D、e1+e2≥2
|
函数y=1-
sinx的单调区间是( )
| 2 |
| 3 |
A、[-
| ||||
B、[-
| ||||
C、[-
| ||||
D、[-
|