题目内容
已知f(x)=x2-2x,x∈[a,b]的值域为[-1,8],则b-a的范围是 .
考点:函数的值域,函数的定义域及其求法
专题:函数的性质及应用
分析:对f(x)配方f(x)=(x-1)2-1,所以看出x=1时,f(x)=-1,令(x-1)2-1=8得x=-2,或4.所以b-a最大为4-(-2)=6,最小为4-1=3,这样即求得了b-a的范围.
解答:
解:f(x)=x2-2x=(x-1)2-1,令(x-1)2-1=8得x=-2,或4;
∴b-a最小时b=1,a=-2或b=4,a=1,∴此时b-a=3;
b-a最大时b=4,a=-2,∴此时b-a=6;
∴3≤b-a≤6,即b-a的范围是[3,6].
故答案为:[3,6].
∴b-a最小时b=1,a=-2或b=4,a=1,∴此时b-a=3;
b-a最大时b=4,a=-2,∴此时b-a=6;
∴3≤b-a≤6,即b-a的范围是[3,6].
故答案为:[3,6].
点评:考查二次函数的值域,及区间长度,也可根据f(x)的图象求b-a的范围会更形象.

练习册系列答案
相关题目
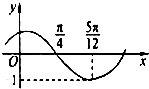 函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<
函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<| π |
| 2 |
A、右平移
| ||
B、左平移
| ||
C、右平移
| ||
D、左平移
|
下列命题错误的是( )
| A、命题“若m≤0,则方程x2+x+m=0有实数根”的逆否命题为:“若方程x2+x+m=0无实数根,则m>0” |
| B、“x=2”是“x2-x-2=0”的充分不必要条件 |
| C、若命题“p且q”为假命题,则命题“p”与命题“q”中必有一真一假 |
| D、对于命题p:存在x∈R,x2+x+1<0,则非p:对任意x∈R,x2+x+1≥0 |