题目内容
锐角α，β满足tanα，tanβ是方程x2-3
x+4=0的两个根，则α+β的值为 ．
| 3 |
考点：两角和与差的正切函数
专题：三角函数的求值
分析：利用韦达定理求得tanα+tanβ和tanα•tanβ的值，进而代入正切的两角和公式求得tan（α+β）的值，进而求得α+β的值．
解答：
解：依题意知tanα+tanβ=3
，tanα•tanβ=4，
∴tan（α+β）=
=
=-
，
∵α，β为锐角，
∴0＜α+β＜π
∴α+β=
，
故答案为：
．
| 3 |
∴tan（α+β）=
| tanα+tanβ |
| 1-tanαtanβ |
3
| ||
| 1-4 |
| 3 |
∵α，β为锐角，
∴0＜α+β＜π
∴α+β=
| 2π |
| 3 |
故答案为：
| 2π |
| 3 |
点评：本题主要考查了两角和与差的正切函数．考查了学生基础知识的综合运用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
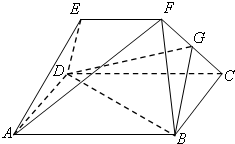如图几何体中，四边形ABCD为矩形，AB=2BC=4，BF=CF=AE=DE，EF=2，EF∥AB，AF⊥CF．
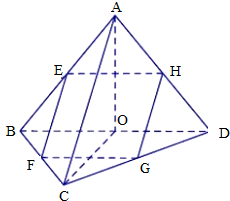在三棱锥A-BCD中，点E、F、G、H分别是AB、BC、CD、DA的中点．