题目内容
设f(x)=log
(10-ax),a为常数,若f(3)=-2.
(1)求a的值;
(2)求使f(x)≥0的x的取值范围;
(3)若对于区间[3,4]上的每一个x的值,不等式f(x)>(
)x+m恒成立,求实数m的取值范围.
| 1 |
| 2 |
(1)求a的值;
(2)求使f(x)≥0的x的取值范围;
(3)若对于区间[3,4]上的每一个x的值,不等式f(x)>(
| 1 |
| 2 |
考点:函数恒成立问题,复合函数的单调性
专题:函数的性质及应用
分析:(1)直接令x=3代入函数f(x)的表达式即可求出a;
(2)f(x)=log
(10-2x),f(x)≥0可化为log
(10-2x)≥0,解此对数不等式即可;
(3)不等式f(x)>(
)x+m恒成立等价于m<log
(10-2x)-(
)x恒成立,令g(x)=log
(10-2x)-(
)x,求m<g(x)最小值即可.
(2)f(x)=log
| 1 |
| 2 |
| 1 |
| 2 |
(3)不等式f(x)>(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(1)f(3)=log
(10-3a)=-2,∴10-3a=(
)-2=4,∴a=2.
(2)f(x)=log
(10-2x),
f(x)≥0可化为log
(10-2x)≥0,
∴0<10-2x≤1,∴
≤x<5,
f(x)≥0的x的取值范围为{x|
≤x<5};
(3)不等式f(x)>(
)x+m恒成立等价于log
(10-2x)>(
)x+m恒成立,也即m<log
(10-2x)-(
)x恒成立,
令g(x)=log
(10-2x)-(
)x,∴m<g(x)最小值即可,
因为函数10-2x递减,函数y=log
x递减,由复合函数的单调性知函数y=log
(10-2x)单调递增,
又因为函数y=-(
)x单调递增,∴g(x)=log
(10-2x)-(
)x单调递增,
∴g(x)在区间[3,4]上的最小值g(x)最小值=g(3)=log
(10-6)-(
)3=-2-
=-
,
∴m<-
.
| 1 |
| 2 |
| 1 |
| 2 |
(2)f(x)=log
| 1 |
| 2 |
f(x)≥0可化为log
| 1 |
| 2 |
∴0<10-2x≤1,∴
| 9 |
| 2 |
f(x)≥0的x的取值范围为{x|
| 9 |
| 2 |
(3)不等式f(x)>(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
令g(x)=log
| 1 |
| 2 |
| 1 |
| 2 |
因为函数10-2x递减,函数y=log
| 1 |
| 2 |
| 1 |
| 2 |
又因为函数y=-(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴g(x)在区间[3,4]上的最小值g(x)最小值=g(3)=log
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 8 |
| 17 |
| 8 |
∴m<-
| 17 |
| 8 |
点评:本题主要考查对数函数及复合函数的性质,复合函数的单调性是解题的关键,同时,不等式恒成立问题常转化为求最值来处理.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
若3x=9,log2
=y,则x+2y等于( )
| 8 |
| 3 |
| A、6 |
| B、8-2log23 |
| C、4 |
| D、log48 |
函数y=
(0<a<1)的图象的大致形状是( )
| xax |
| |x| |
A、 |
B、 |
C、 |
D、 |
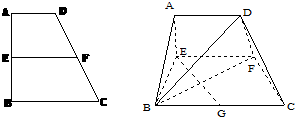 已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=
已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=