题目内容
10.已知向量$\overrightarrow{OB}$=(2,0),向量$\overrightarrow{OC}$=(2,2),向量$\overrightarrow{CA}$=($\sqrt{2}$cosα,$\sqrt{2}$sinα),则向量$\overrightarrow{OA}$与向量$\overrightarrow{CB}$的夹角的取值范围是[105°,165°].分析 根据|CA|=$\sqrt{2}$得出A的轨迹,结合图形可知当OA与轨迹圆相切时,夹角取得最值,利用平面几何的性质求出切线的夹角即可得出向量的夹角.
解答 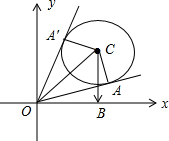 解:∵$\overrightarrow{OB}$=(2,0),$\overrightarrow{OC}$=(2,2),∴B(2,0),C(2,2),
解:∵$\overrightarrow{OB}$=(2,0),$\overrightarrow{OC}$=(2,2),∴B(2,0),C(2,2),
∵$\overrightarrow{CA}$=($\sqrt{2}$cosα,$\sqrt{2}$sinα),∴|$\overrightarrow{CA}$|=$\sqrt{2}$,
∴A在以C为圆心,以$\sqrt{2}$为半径的圆C上.
∴当OA与圆C相切时,向量$\overrightarrow{OA}$与向量$\overrightarrow{CB}$的夹角取得最大值或最小值.
设切点分别为A和A′,连结OC,OA,OA′,则OC=2$\sqrt{2}$,AC⊥OA,
∵sin∠AOC=$\frac{AC}{OC}=\frac{1}{2}$,∴∠AOC=∠A′OC=30°,
∴∠AOB=∠AOy=15°,
∴当切点为A时,向量$\overrightarrow{OA}$与向量$\overrightarrow{CB}$的夹角取得最小值15°+90°=105°,
当切点为A′时,向量$\overrightarrow{OA}$与向量$\overrightarrow{CB}$的夹角取得最大值180°-15°=165°.
故答案为:[105°,165°].
点评 本题考查了平面向量的几何意义,向量夹角的运算,属于中档题.

练习册系列答案
相关题目
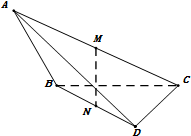 如图,在三棱锥A-BCD中,二面角A-BC-D的大小为$\frac{π}{4}$,AB⊥BC,DC⊥BC,M,N分别为AC,BD的中点,已知AB=$\sqrt{2}$,BC=CD=1.
如图,在三棱锥A-BCD中,二面角A-BC-D的大小为$\frac{π}{4}$,AB⊥BC,DC⊥BC,M,N分别为AC,BD的中点,已知AB=$\sqrt{2}$,BC=CD=1.