题目内容
1.设函数f(x)=-ln(-x+1);g(x)=$\left\{\begin{array}{l}{x^2}({x≥0})\\ f(x)({x<0})\end{array}$,则g(-2)=-ln3;函数y=g(x)+1的零点是1-e.分析 g(-2)=f(-2),令g(x)=-1,对x进行讨论,列方程组解出x即可.
解答 解:∵当x<0时,g(x)=f(x),
∴g(-2)=f(-2)=-ln3.
令y=g(x)+1=0得g(x)=-1,
∴$\left\{\begin{array}{l}{{x}^{2}=-1}\\{x≥0}\end{array}\right.$或$\left\{\begin{array}{l}{-ln(-x+1)=-1}\\{x<0}\end{array}\right.$,
解得x=1-e.
故答案为:-ln3,1-e.
点评 本题考查了分段函数函数值的计算,函数零点的计算,属于中档题.

练习册系列答案
相关题目
8.若直线(1+a)x+y+1=0与圆(x-1)2+y2=1相切,则a的值为( )
| A. | 1,-1 | B. | 2,-2 | C. | 1 | D. | -1 |
13.设α,β是第二象限的角,且sinα<sinβ,那么下列不等式成立的是( )
| A. | α<β | B. | cosα<cosβ | C. | tanα<tanβ | D. | sinα>sinβ |
6.如图,ABCD-A1B1C1D1为正方体,则下列结论错误的是( )
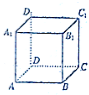

| A. | A1C⊥B1D1 | B. | B1D1∥平面BDC1 | ||
| C. | A1C⊥平面BDC1 | D. | 异面直线AD与BC1所成的角为30° |