题目内容
2.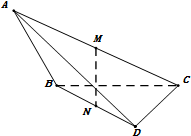 如图,在三棱锥A-BCD中,二面角A-BC-D的大小为$\frac{π}{4}$,AB⊥BC,DC⊥BC,M,N分别为AC,BD的中点,已知AB=$\sqrt{2}$,BC=CD=1.
如图,在三棱锥A-BCD中,二面角A-BC-D的大小为$\frac{π}{4}$,AB⊥BC,DC⊥BC,M,N分别为AC,BD的中点,已知AB=$\sqrt{2}$,BC=CD=1.(Ⅰ)求证:MN⊥面BCD;
(Ⅱ)求直线AD与平面BCD所成角的大小.
分析 (I)取BC中点E,连接ME,NE,利用线面垂直的判定定理可得ME⊥BC,同理NE⊥BC,利用线面垂直的判定与性质定理可得BC⊥MN,可得∠MEN为二面角A-BC-D的平面角,利用余弦定理与勾股定理的逆定理即可得出.
(II)取DC中点P,连接MP,NP,可得MP⊥AD,由(1)知MN⊥平面BCD,于是∠MPN为所求的线面角.利用直角三角形的边角关系即可得出.
解答 (I)证明:取BC中点E,连接ME,NE,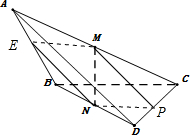
则ME⊥AB,AB⊥BC,可得ME⊥BC,
同理NE⊥BC,又ME∩NE=E,
∴BC⊥平面MNE,∴BC⊥MN,
∴∠MEN为二面角A-BC-D的平面角,∴∠MEN=45°,
∴在△MEN中,ME=$\frac{1}{2}$AB=$\frac{\sqrt{2}}{2}$,NE=$\frac{1}{2}$DC=$\frac{1}{2}$,
∴MN=$\sqrt{M{E}^{2}+N{E}^{2}-2ME•NEcos4{5}^{°}}$=$\frac{1}{2}$,
∴MN2+NE2=ME2,MN⊥NE,∴MN⊥面BCD.
(II)解:取DC中点P,连接MP,NP,
则MP⊥AD,由(1)知MN⊥平面BCD,则∠MPN为所求的线面角.
∵NP=$\frac{1}{2}$BC=$\frac{1}{2}$,在RT△MNP中,MN=NP=$\frac{1}{2}$,∠MPN45°.
即直线AD与平面BCD所成角为45°.
点评 本题考查了线面面面垂直的判定与性质定理、空间角、余弦定理、直角三角形的边角关系,考查了空间想象能力、推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
17.设$\overrightarrow{{e}_{1}}$与$\overrightarrow{{e}_{2}}$是两个不共线的向量,$\overrightarrow{AB}$=$\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$,$\overrightarrow{CB}$=k$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$,$\overrightarrow{CD}$=3$\overrightarrow{{e}_{1}}$-2k$\overrightarrow{{e}_{2}}$,若A,B,D共线,则k的值为( )
| A. | -$\frac{9}{4}$ | B. | -$\frac{4}{9}$ | C. | -$\frac{3}{8}$ | D. | 不存在 |
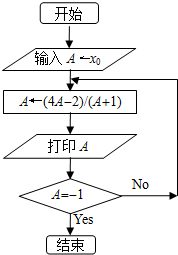 若根据如图的框图,产生数列{an}.
若根据如图的框图,产生数列{an}.