题目内容
2.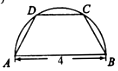 如图,将一块半径为2的半圆形纸板切割成等腰梯形的形状,下底AB是半圆的直径,上底CD的端点在半圆上,则所得梯形的周长的最大值为10.
如图,将一块半径为2的半圆形纸板切割成等腰梯形的形状,下底AB是半圆的直径,上底CD的端点在半圆上,则所得梯形的周长的最大值为10.
分析 画出图形,并分别过C,D作AB的垂线,垂足分别为F,E,可设∠EOD=θ($θ∈(0,\frac{π}{2})$),从而得出CD=4cosθ,$BC=AD=2\sqrt{2-2cosθ}$=$4sin\frac{θ}{2}$,这便可得出梯形的周长,换元:令$sin\frac{θ}{2}=t$,得到关于t的二次函数,配方即可求出周长的最大值.
解答 解:如图所示,分别过C,D,作CF⊥AB,DE⊥AB,垂足为F,E;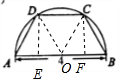
则四边形CDEF为矩形;
设∠EOD=θ∈$(0,\frac{π}{2})$;
可得:CD=2OE=4cosθ,ED=2sinθ,AE=2-2cosθ;
∴BC=AD=$\sqrt{(2sinθ)^{2}+(2-2cosθ)^{2}}$=2$\sqrt{2-2cosθ}$;
∴梯形的周长=4+4cosθ+4$\sqrt{2-2cosθ}$=8$sin\frac{θ}{2}$+4($1-2si{n}^{2}\frac{θ}{2}$)+4;
令$sin\frac{θ}{2}$=t∈$(0,\frac{\sqrt{2}}{2})$,则:
f(t)=-8t2+8t+8=$-8(t-\frac{1}{2})^{2}+10$;
∴t=$\frac{1}{2}$时,梯形的周长取最大值10.
故答案为:10.
点评 考查直角三角形边的关系,数形结合解题的方法,二倍角的余弦公式,配方求二次函数最值的方法.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
5.下列函数中为奇函数的是( )
| A. | y=x+cosx | B. | y=x+sinx | C. | $y=\sqrt{x}$ | D. | y=e-|x| |
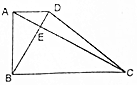
 如图,棱柱ABCD-A1B1C1D1中,底面ABCD是平行四边形,侧棱AA1⊥底面ABCD,AB=1,AC=$\sqrt{3}$,BC=BB1=2.
如图,棱柱ABCD-A1B1C1D1中,底面ABCD是平行四边形,侧棱AA1⊥底面ABCD,AB=1,AC=$\sqrt{3}$,BC=BB1=2.