��Ŀ����
11����֪����װ�д�С��ͬ��2������2�������1������һ����Ϸ�涨��ÿ��������ͻ���ķ�ֵ�ֱ���0�֡�1�ֺ�2�֣�ÿһ�ִӴ���һ����ȡ��������3�����Ӧ�ķ�ֵ��Ӻ��Ϊ�þֵĵ÷֣�������÷ֺ���Żش��У������ֵ�n�ֵ�n��n��N*���ֵ����������Ϸ���أ�ͬʱ��Ϸ���������ľֹ�����δ���أ���ϷҲ��������1������һ����Ϸ�е�3�ֵĸ��ʣ�
��2������Ϸ����ʱ����X�ķֲ��к���ѧ����E��X����
���� ������������¼��ĸ��ʹ�ʽ�����Ӧ�ĸ���ֵ��
����������֪�������X�Ŀ���ȡֵ��������һ����Ϸ�е�2�ֵĸ���ֵ��
�����Ӧ�ĸ���ֵ��д���ֲ��У�������ѧ������
��� �⣺��������һ����Ϸ�е�3��Ϊ�¼�A��
��P��A��=$\frac{{C}_{2}^{1}{•C}_{2}^{1}{•C}_{1}^{1}}{{C}_{5}^{3}}$=$\frac{2}{5}$��
�����������������X�Ŀ���ȡֵΪ1��2��3��4��
����һ����Ϸ�е�2�ֵĸ���Ϊ$\frac{{C}_{2}^{1}{•C}_{2}^{2}{+C}_{2}^{2}{•C}_{1}^{1}}{{C}_{5}^{3}}$=$\frac{3}{10}$��
��P��X=1��=$\frac{{C}_{2}^{2}{•C}_{2}^{1}}{{C}_{5}^{3}}$=$\frac{1}{5}$��
P��X=2��=$\frac{4}{5}$��$\frac{3}{10}$=$\frac{6}{25}$��
P��X=3��=$\frac{4}{5}$����1-$\frac{3}{10}$����$\frac{2}{5}$=$\frac{28}{125}$��
P��X=4��=$\frac{4}{5}$����1-$\frac{3}{10}$����$\frac{3}{5}$=$\frac{42}{125}$��
��X�ķֲ���Ϊ��
| X | 1 | 2 | 3 | 4 |
| P | $\frac{1}{5}$ | $\frac{6}{25}$ | $\frac{28}{125}$ | $\frac{42}{125}$ |
���� ���⿼����������¼������Լ���ɢ����������ķֲ��к���ѧ�����ļ������⣬���е��⣮

| A�� | A=B | B�� | B?A | C�� | A?B | D�� | A��B=∅ |
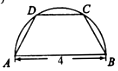 ��ͼ����һ��뾶Ϊ2�İ�Բ��ֽ���и�ɵ������ε���״���µ�AB�ǰ�Բ��ֱ�����ϵ�CD�Ķ˵��ڰ�Բ�ϣ����������ε��ܳ������ֵΪ10��
��ͼ����һ��뾶Ϊ2�İ�Բ��ֽ���и�ɵ������ε���״���µ�AB�ǰ�Բ��ֱ�����ϵ�CD�Ķ˵��ڰ�Բ�ϣ����������ε��ܳ������ֵΪ10��