题目内容
14.已知Sn为数列{an}的前n项和,an=2•3n-1(n∈N*),若bn=$\frac{{a}_{n+1}}{{S}_{n}{S}_{n+1}}$,则b1+b2+…bn=$\frac{1}{2}$-$\frac{1}{{3}^{n+1}-1}$.分析 an=2•3n-1(n∈N*),可得Sn=$\frac{2({3}^{n}-1)}{3-1}$=3n-1.可得:bn=$\frac{{a}_{n+1}}{{S}_{n}{S}_{n+1}}$=$\frac{2×{3}^{n}}{({3}^{n}-1)({3}^{n+1}-1)}$=$\frac{1}{{3}^{n}-1}$-$\frac{1}{{3}^{n+1}-1}$,再利用裂项求和方法即可得出.
解答 解:an=2•3n-1(n∈N*),∴Sn=$\frac{2({3}^{n}-1)}{3-1}$=3n-1.
∴bn=$\frac{{a}_{n+1}}{{S}_{n}{S}_{n+1}}$=$\frac{2×{3}^{n}}{({3}^{n}-1)({3}^{n+1}-1)}$=$\frac{1}{{3}^{n}-1}$-$\frac{1}{{3}^{n+1}-1}$,
则b1+b2+…bn=$(\frac{1}{2}-\frac{1}{{3}^{2}-1})$+$(\frac{1}{{3}^{2}-1}-\frac{1}{{3}^{3}-1})$+…+$(\frac{1}{{3}^{n}-1}-\frac{1}{{3}^{n+1}-1})$=$\frac{1}{2}$-$\frac{1}{{3}^{n+1}-1}$,
故答案为:$\frac{1}{2}$-$\frac{1}{{3}^{n+1}-1}$.
点评 本题考查了数列递推关系、等比数列的通项公式与求和公式、裂项求和方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
5.在△ABC中,a,b,c分别是角A、B、C所对的边长,A、B均为锐角,若sinA=cosB,则$\frac{a+b}{c}$的最大值是( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
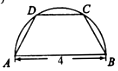 如图,将一块半径为2的半圆形纸板切割成等腰梯形的形状,下底AB是半圆的直径,上底CD的端点在半圆上,则所得梯形的周长的最大值为10.
如图,将一块半径为2的半圆形纸板切割成等腰梯形的形状,下底AB是半圆的直径,上底CD的端点在半圆上,则所得梯形的周长的最大值为10. 如图,在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,PA=2,AB=1.
如图,在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,PA=2,AB=1.