题目内容
12. 如图,棱柱ABCD-A1B1C1D1中,底面ABCD是平行四边形,侧棱AA1⊥底面ABCD,AB=1,AC=$\sqrt{3}$,BC=BB1=2.
如图,棱柱ABCD-A1B1C1D1中,底面ABCD是平行四边形,侧棱AA1⊥底面ABCD,AB=1,AC=$\sqrt{3}$,BC=BB1=2.(Ⅰ)求证:AC⊥平面ABB1A1;
(Ⅱ)求点D到平面ABC1的距离d.
分析 (I)利用勾股定理逆定理证明AC⊥AB,结合AC⊥AA1可得AC平面ABB1A1.
(II)根据V${\;}_{{C}_{1}-ABD}$=V${\;}_{D-AB{C}_{1}}$,列方程解出d.
解答 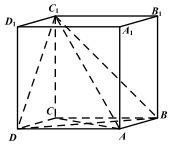 (Ⅰ)证明:∵在底面ABCD中,AB=1,$AC=\sqrt{3}$,BC=2,
(Ⅰ)证明:∵在底面ABCD中,AB=1,$AC=\sqrt{3}$,BC=2,
∴BC2=AC2+AB2,即AB⊥AC,
∵侧棱AA1⊥底面ABCD,AC?平面ABCD,
∴AA1⊥AC,
又∵AA1∩AB=A,AA1?平面ABB1A1,AB?平面ABB1A1,
∴AC⊥平面ABB1A1.
(Ⅱ)连接DB,DC1,
由(Ⅰ)知△ABC为直角三角形,且${S_{△ABC}}=\frac{1}{2}×1×\sqrt{3}=\frac{{\sqrt{3}}}{2}$,
∴S△ABD=$\frac{1}{2}$S${\;}_{平行四边形AB{C}_{1}{D}_{1}}$=S△ABC=$\frac{\sqrt{3}}{2}$,
又∵侧棱CC1⊥底面ABCD,
∴${V_{{C_1}-ABD}}=\frac{1}{3}×{S_{△ABD}}×C{C_1}=\frac{{\sqrt{3}}}{3}$,
∵AB⊥AC,AB⊥CC1,AC∩CC1=C,
∴AB⊥平面ACC1,且AC1?平面ACC1,
∴AB⊥AC1,
又∵$A{C_1}=\sqrt{A{C^2}+C{C_1}^2}=\sqrt{7}$,
∴${S_{△AB{C_1}}}=\frac{1}{2}×1×\sqrt{7}=\frac{{\sqrt{7}}}{2}$,
∴${V_{D-AB{C_1}}}=\frac{1}{3}×{S_{△AB{C_1}}}×d$=${V_{{C_1}-ABD}}=\frac{{\sqrt{3}}}{3}$,
解得$d=\frac{{2\sqrt{21}}}{7}$.
点评 本题考查了线面垂直的判定,空间距离的计算,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | A=B | B. | B?A | C. | A?B | D. | A∩B=∅ |
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $-\frac{3}{4}$ | D. | $-\frac{4}{3}$ |
| A. | [-1,+∞) | B. | (-1,+∞) | C. | [-$\frac{1}{2}$,+∞) | D. | R |
| A. | (-∞,2-$\sqrt{2}$] | B. | [2-$\sqrt{2}$,+∞) | C. | (-∞,2-$\sqrt{2}$) | D. | (2-$\sqrt{2}$,+∞) |
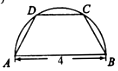 如图,将一块半径为2的半圆形纸板切割成等腰梯形的形状,下底AB是半圆的直径,上底CD的端点在半圆上,则所得梯形的周长的最大值为10.
如图,将一块半径为2的半圆形纸板切割成等腰梯形的形状,下底AB是半圆的直径,上底CD的端点在半圆上,则所得梯形的周长的最大值为10.