题目内容
10.已知正方体ABCD-A1B1C1D1内有一个内切球O,则在正方体ABCD-A1B1C1D1内任取点M,求点M在球O内的概率.分析 本题是几何概型问题,欲求点M在球O内的概率,先由正方体ABCD-A1B1C1D1内的内切球O,求出其体积,再根据几何概型概率公式结合正方体的体积的方法易求解.
解答 解:本题是几何概型问题,设正方体的棱长为:2.
正方体ABCD-A1B1C1D1内的内切球O的半径是其棱长的一半,其体积为:V1=$\frac{4}{3}$π×13=$\frac{4}{3}$π,
则点M在球O内的概率是$\frac{\frac{4π}{3}}{8}$=$\frac{π}{6}$.
点评 本小题主要考查几何概型的应用、几何体和体积等基础知识,考查空间想象能力、化归与转化思想.属于中档题.

练习册系列答案
相关题目
5.在△ABC中,a,b,c分别是角A、B、C所对的边长,A、B均为锐角,若sinA=cosB,则$\frac{a+b}{c}$的最大值是( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
20.已知集合A={x|x>1},B={y|y=x2,x∈R},则( )
| A. | A=B | B. | B?A | C. | A?B | D. | A∩B=∅ |
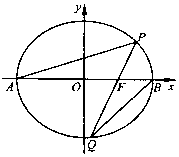 如图,在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的左、右顶点分别为A,B,过右焦点F的直线l与椭圆C交于P,Q两点(点P在x轴上方).
如图,在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的左、右顶点分别为A,B,过右焦点F的直线l与椭圆C交于P,Q两点(点P在x轴上方).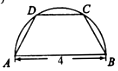 如图,将一块半径为2的半圆形纸板切割成等腰梯形的形状,下底AB是半圆的直径,上底CD的端点在半圆上,则所得梯形的周长的最大值为10.
如图,将一块半径为2的半圆形纸板切割成等腰梯形的形状,下底AB是半圆的直径,上底CD的端点在半圆上,则所得梯形的周长的最大值为10.