题目内容
6.已知函数f(x)=1nx+2x-6的零点在区间($\frac{k}{2}$,$\frac{k+1}{2}$)(k∈Z)内,那么k=5.分析 函数f(x)=lnx+2x-6在其定义域上连续单调递增,从而利用函数的零点的判定定理求解即可.
解答 解:函数f(x)=lnx+2x-6在其定义域(0,+∞)上连续单调递增,
f(1)=ln1+2-6=-4<0
f(2)=ln2+4-6=ln2-2<0,
f(3)=ln3+6-6=ln3>0;
∴根据零点存在定理,?x0∈(2,3),使得f(x0)=0.
∵f($\frac{5}{2}$)=ln$\frac{5}{2}$-1=ln$\frac{5}{2}$-lne<0
∴x0∈($\frac{5}{2}$,3)
∴$\frac{k}{2}$=$\frac{5}{2}$即k=5
故答案为:5.
点评 本题考查了函数的零点的判定定理的应用.注意函数的单调性以及函数的连续性的判断.

练习册系列答案
相关题目
5.在△ABC中,a,b,c分别是角A、B、C所对的边长,A、B均为锐角,若sinA=cosB,则$\frac{a+b}{c}$的最大值是( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
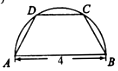 如图,将一块半径为2的半圆形纸板切割成等腰梯形的形状,下底AB是半圆的直径,上底CD的端点在半圆上,则所得梯形的周长的最大值为10.
如图,将一块半径为2的半圆形纸板切割成等腰梯形的形状,下底AB是半圆的直径,上底CD的端点在半圆上,则所得梯形的周长的最大值为10.