题目内容
已知函数f(x)=
且f′(1)=2,则实数a的值为( )
| ax2-1 |
| A、1 | ||
| B、2 | ||
C、
| ||
| D、a>0 |
考点:导数的运算
专题:导数的概念及应用
分析:求函数的导数,根据导数进行求解即可.
解答:
解:函数的导数f′(x)=
=
,
∵f′(1)=2,
∴f′(1)=
=2,
则a>0,
解得a=2,
故选:B
| 2ax | ||
2
|
| ax | ||
|
∵f′(1)=2,
∴f′(1)=
| a | ||
|
则a>0,
解得a=2,
故选:B
点评:本题主要考查导数的计算,要求熟练掌握常见函数的导数公式以及导数的运算法则.

练习册系列答案
相关题目
用秦九韶算法计算多项式f(x)=2x5-3x4+7x3-9x2+4x-10在x=2时的值时,V3的值为( )
| A、34 | B、22 | C、9 | D、1 |
函数f(x)是定义在R上的奇函数,当x<0时,f(x)=(
)x,则函数f(x)的反函数的零点为( )
| 1 |
| 3 |
| A、2 | B、-2 | C、3 | D、0 |
计算:[(-
)2]-1=( )
| 2 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|
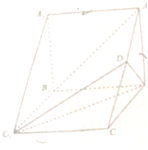 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,△ABC是等边三角形,D为AC的中点,AA1=AB=2.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,△ABC是等边三角形,D为AC的中点,AA1=AB=2.