题目内容
某班从6名班干部(其中男生4人,女生2人)中,任选3人参加学校的义务劳动.
(1)设所选3人中女生人数为X,求X的分布列;
(2)求男生甲或女生乙被选中的概率;
(3)设“男生甲被选中”为事件A,“女生乙被选中”为事件B,求P(B|A).
(1)设所选3人中女生人数为X,求X的分布列;
(2)求男生甲或女生乙被选中的概率;
(3)设“男生甲被选中”为事件A,“女生乙被选中”为事件B,求P(B|A).
考点:条件概率与独立事件,离散型随机变量及其分布列
专题:应用题,概率与统计
分析:(1)由题设知,X的可有取值为0,1,2,分别求出相应的概率,由此能求出X的分布列;
(2)利用对立事件的概率公式求解即可;
(3)求出男生甲被选中的概率、男生甲、女生乙都被选中的概率,即可得出结论.
(2)利用对立事件的概率公式求解即可;
(3)求出男生甲被选中的概率、男生甲、女生乙都被选中的概率,即可得出结论.
解答:
解:(1)X=0、1、2、3…(1分),
P(X=0)=
=
,P(X=1)=
=
,P(X=2)=
=
.
∴ξ的分布列为:
…(4分)
(2)P=1-
=1-
=
…(8分)
(3)P(A)=
=
,P(AB)=
=
,P(B|A)=
…(12分)
P(X=0)=
| ||
|
| 1 |
| 5 |
| ||||
|
| 3 |
| 5 |
| ||||
|
| 1 |
| 5 |
∴ξ的分布列为:
| X | 0 | 1 | 2 | ||||||
| P |
|
|
|
(2)P=1-
| ||
|
| 1 |
| 5 |
| 4 |
| 5 |
(3)P(A)=
| ||
|
| 1 |
| 2 |
| ||
|
| 1 |
| 5 |
| 2 |
| 5 |
点评:本题考查离散型随机变量的分布列,查了随机事件的概率和条件概率公式等知识,考查学生的计算能力,属于中档题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
记等差数列{an}的前n项和为Sn,若a1=
,S4=20,则S6=( )
| 1 |
| 2 |
| A、12 | B、24 | C、48 | D、96 |
如果执行如图的程序框图,输出的n的值为( )


| A、8 | B、9 | C、.10 | D、11 |
 如图所示是某学校一名篮球运动员在五场比赛中所得分数的茎叶图,则该运动员在这五场比赛中得分的方差为 (注:方差s2=
如图所示是某学校一名篮球运动员在五场比赛中所得分数的茎叶图,则该运动员在这五场比赛中得分的方差为 (注:方差s2=| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
. |
| x |
| A、5.8 | B、6.8 |
| C、7.8 | D、8.8 |
从一箱产品中随机地抽取一件,设事件A={抽到一等品},事件B={抽到二等品},事件C={抽到三等品},且已知 P(A)=0.65,P(B)=0.2,P(C)=0.1.则事件“抽到的不是一等品”的概率为( )
| A、0.7 | B、0.65 |
| C、0.35 | D、0.3 |
已知函数f(x)=
且f′(1)=2,则实数a的值为( )
| ax2-1 |
| A、1 | ||
| B、2 | ||
C、
| ||
| D、a>0 |
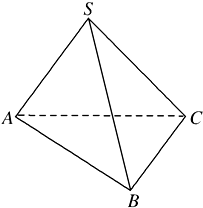 如图所示,在三棱锥S-ABC中,SA⊥SB,SB⊥SC,SC⊥SA,且SA,SB,SC和底面ABC所成的角分别为α1,α2,α3,△SBC,△SAC,△SAB的面积分别为S1,S2,S3,类比三角形中的正弦定理,给出空间图形的一个猜想是
如图所示,在三棱锥S-ABC中,SA⊥SB,SB⊥SC,SC⊥SA,且SA,SB,SC和底面ABC所成的角分别为α1,α2,α3,△SBC,△SAC,△SAB的面积分别为S1,S2,S3,类比三角形中的正弦定理,给出空间图形的一个猜想是