题目内容
12.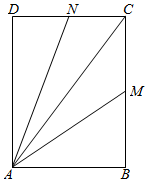 如图,矩形ABCD中,AB=3,AD=4,M、N分别为线段BC、CD上的点,且满足$\frac{1}{C{M}^{2}}$$+\frac{1}{C{N}^{2}}$=1,若$\overrightarrow{AC}$=x$\overrightarrow{AM}$+y$\overrightarrow{AN}$,则x+y的最小值为$\frac{5}{4}$.
如图,矩形ABCD中,AB=3,AD=4,M、N分别为线段BC、CD上的点,且满足$\frac{1}{C{M}^{2}}$$+\frac{1}{C{N}^{2}}$=1,若$\overrightarrow{AC}$=x$\overrightarrow{AM}$+y$\overrightarrow{AN}$,则x+y的最小值为$\frac{5}{4}$.
分析 由题意建立如图所示坐标系,设点M(3,a),N(b,4),0<a<4,0<b<3;从而可得b=$\frac{3-3x}{y}$,a=$\frac{4-4y}{x}$,从而可得$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=(x+y-1)2,设x+y=m,则x=m-y;从而利用判别式求解.
解答 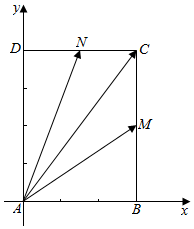 解:由题意建立如图所示坐标系,
解:由题意建立如图所示坐标系,
设点M(3,a),N(b,4),0<a<4,0<b<3;
∵$\overrightarrow{AC}$=(3,4),$\overrightarrow{AM}$=(3,a),$\overrightarrow{AN}$=(b,4);
又∵$\overrightarrow{AC}$=x$\overrightarrow{AM}$+y$\overrightarrow{AN}$,
∴(3,4)=x(3,a)+y(b,4),
即$\left\{\begin{array}{l}{3=3x+yb}\\{4=xa+4y}\end{array}\right.$,
∴b=$\frac{3-3x}{y}$,a=$\frac{4-4y}{x}$,
∴$\frac{1}{C{M}^{2}}$=$\frac{1}{(4-a)^{2}}$=$\frac{1}{16}$$\frac{{x}^{2}}{(x+y-1)^{2}}$,$\frac{1}{C{N}^{2}}$=$\frac{1}{9}$$\frac{{y}^{2}}{(x+y-1)^{2}}$,
∴$\frac{1}{16}$$\frac{{x}^{2}}{(x+y-1)^{2}}$+$\frac{1}{9}$$\frac{{y}^{2}}{(x+y-1)^{2}}$=1,
即$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=(x+y-1)2,
设x+y=m,则x=m-y;
则$\frac{(m-y)^{2}}{16}$+$\frac{{y}^{2}}{9}$=(m-1)2,
即25y2-18my+9m2-144(m-1)2=0,
故△=(18m)2-4×25×(9m2-144(m-1)2)≥0,
即24m2-50m+25≥0,
解得,m≥$\frac{5}{4}$或m≤$\frac{5}{6}$(舍去);
故答案为:$\frac{5}{4}$.
点评 本题考查了平面向量的应用,同时考查了数形结合的思想与方程思想的应用,属于中档题.

| A. | lna<-2b | B. | lna≤-2b | C. | lna>-2b | D. | lna≥-2b |
| A. | 右平移$\frac{5π}{12}$个单位 | B. | 右平移$\frac{π}{12}$个单位 | ||
| C. | 左平移$\frac{π}{6}$个单位 | D. | 左平移$\frac{π}{12}$个单位 |
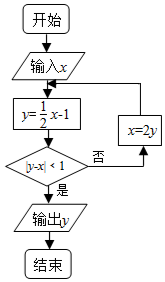
| A. | 0 | B. | -1 | C. | -$\frac{3}{2}$ | D. | -3 |
| A. | 25 | B. | 35 | C. | 45 | D. | 55 |

| A. | $\frac{1}{8}$ | B. | 1 | C. | 2 | D. | 4 |