题目内容
2.设集合M={x|x2=x},N={x|log2x≤0},则M∪N=[0,1].分析 求出M中方程的解确定出M,求出N中不等式的解集确定出N,找出两集合的并集即可.
解答 解:由M中方程变形得:x(x-1)=0,
解得:x=0或x=1,即M={0,1},
由N中不等式变形得:log2x≤0=log21,即0<x≤1,
∴N=(0,1],
则M∪N=[0,1],
故答案为:[0,1]
点评 此题考查了并集及其运算,熟练掌握并集的定义是解本题的关键.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
10.若tanα=1,则sin2α-cos2α的值为( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
17.某工厂有两条相互不影响的生产线分别生产甲、乙两种产品,产品出厂前需要对产品进行性能检测.检测得分低于80的为不合格品,只能报废回收;得分不低于80的为合格品,可以出厂.现随机抽取这两种产品各60件进行检测,检测结果统计如表:
(Ⅰ)试分别估计产品甲,乙下生产线时为合格品的概率;
(Ⅱ)生产一件产品甲,若是合格品可盈利100元,若是不合格品则亏损20元;生产一件产品乙,若是合格品可盈利90元,若是不合格品则亏损15元.在(Ⅰ)的前提下:
(1)记X为生产1件甲和1件乙所得的总利润,求随机变量X的分布列和数学期望;
(2)求生产5件乙所获得的利润不少于300元的概率.
| 得分 | [60,70) | [70,80) | [80,90) | [90,100] |
| 甲 | 5 | 10 | 34 | 11 |
| 乙 | 8 | 12 | 31 | 9 |
(Ⅱ)生产一件产品甲,若是合格品可盈利100元,若是不合格品则亏损20元;生产一件产品乙,若是合格品可盈利90元,若是不合格品则亏损15元.在(Ⅰ)的前提下:
(1)记X为生产1件甲和1件乙所得的总利润,求随机变量X的分布列和数学期望;
(2)求生产5件乙所获得的利润不少于300元的概率.
12.已知函数数f(x)=sin(ωx-$\frac{π}{6}$)+$\frac{1}{2}$,x∈R,且f(α)=-$\frac{1}{2}$,f(β)=$\frac{1}{2}$,若|α-β|的最小值为$\frac{3π}{4}$,则函数的单调递增区为( )
| A. | [-$\frac{π}{2}$+2kπ,π+2kπ],k∈Z | B. | [-$\frac{π}{2}$+3kπ,π+3kπ],k∈Z | ||
| C. | [π+2kπ,$\frac{5}{2}$π+2kπ],k∈Z | D. | [π+3kπ,$\frac{5}{2}$π+3kπ],k∈Z |
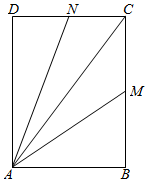 如图,矩形ABCD中,AB=3,AD=4,M、N分别为线段BC、CD上的点,且满足$\frac{1}{C{M}^{2}}$$+\frac{1}{C{N}^{2}}$=1,若$\overrightarrow{AC}$=x$\overrightarrow{AM}$+y$\overrightarrow{AN}$,则x+y的最小值为$\frac{5}{4}$.
如图,矩形ABCD中,AB=3,AD=4,M、N分别为线段BC、CD上的点,且满足$\frac{1}{C{M}^{2}}$$+\frac{1}{C{N}^{2}}$=1,若$\overrightarrow{AC}$=x$\overrightarrow{AM}$+y$\overrightarrow{AN}$,则x+y的最小值为$\frac{5}{4}$.