题目内容
7.一个算法的流程图如图所示,若输入x的值为1,则输出y的值是( )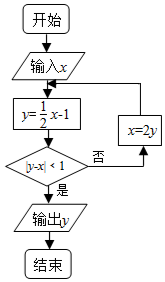
| A. | 0 | B. | -1 | C. | -$\frac{3}{2}$ | D. | -3 |
分析 由已知中的程序框图可知:该程序的功能是利用循环结构计算并输出变量y的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.
解答 解:第一次执行循环体后,y=-$\frac{1}{2}$,不满足退出循环的条件,故x=-1,
第二次执行循环体后,y=-$\frac{3}{2}$,满足退出循环的条件,故x=-1,
故输出的y值为-$\frac{3}{2}$,
故选:C
点评 本题考查的知识点是程序框图,当循环的次数不多,或有规律时,常采用模拟循环的方法解答.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
5.若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1上一点与其左顶点、右焦点构成以右焦点为直角顶点的等腰三角形,则此双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 2$+\sqrt{2}$ |
2.(a+b+c)10的展开式中,合并同类项后不同的项有( )
| A. | 66 | B. | 78 | C. | 105 | D. | 120 |
17.某工厂有两条相互不影响的生产线分别生产甲、乙两种产品,产品出厂前需要对产品进行性能检测.检测得分低于80的为不合格品,只能报废回收;得分不低于80的为合格品,可以出厂.现随机抽取这两种产品各60件进行检测,检测结果统计如表:
(Ⅰ)试分别估计产品甲,乙下生产线时为合格品的概率;
(Ⅱ)生产一件产品甲,若是合格品可盈利100元,若是不合格品则亏损20元;生产一件产品乙,若是合格品可盈利90元,若是不合格品则亏损15元.在(Ⅰ)的前提下:
(1)记X为生产1件甲和1件乙所得的总利润,求随机变量X的分布列和数学期望;
(2)求生产5件乙所获得的利润不少于300元的概率.
| 得分 | [60,70) | [70,80) | [80,90) | [90,100] |
| 甲 | 5 | 10 | 34 | 11 |
| 乙 | 8 | 12 | 31 | 9 |
(Ⅱ)生产一件产品甲,若是合格品可盈利100元,若是不合格品则亏损20元;生产一件产品乙,若是合格品可盈利90元,若是不合格品则亏损15元.在(Ⅰ)的前提下:
(1)记X为生产1件甲和1件乙所得的总利润,求随机变量X的分布列和数学期望;
(2)求生产5件乙所获得的利润不少于300元的概率.
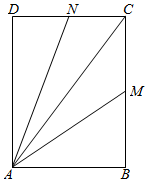 如图,矩形ABCD中,AB=3,AD=4,M、N分别为线段BC、CD上的点,且满足$\frac{1}{C{M}^{2}}$$+\frac{1}{C{N}^{2}}$=1,若$\overrightarrow{AC}$=x$\overrightarrow{AM}$+y$\overrightarrow{AN}$,则x+y的最小值为$\frac{5}{4}$.
如图,矩形ABCD中,AB=3,AD=4,M、N分别为线段BC、CD上的点,且满足$\frac{1}{C{M}^{2}}$$+\frac{1}{C{N}^{2}}$=1,若$\overrightarrow{AC}$=x$\overrightarrow{AM}$+y$\overrightarrow{AN}$,则x+y的最小值为$\frac{5}{4}$.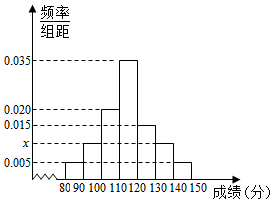 40名高三学生某次数学考试成绩(单位:分)的频率分布直方图如图:
40名高三学生某次数学考试成绩(单位:分)的频率分布直方图如图: