题目内容

4．设等差数列{an}的前n项和为Sn，且a2+a4+a6=15，则S7=（　　）
A．25B．35C．45D．55

分析 根据题意，等差数列{an}中，有a2+a4+a6=15，结合等差数列的性质可得a4=5，进而由等差数列前n项和公式可得S7=$\frac{（{a}_{1}+{a}_{7}）×7}{2}$=7a4，代入a4=5即可得答案．

解答 解：根据题意，等差数列{an}中，有a2+a4+a6=15，则3a4=15，即a4=5，
则S7=$\frac{（{a}_{1}+{a}_{7}）×7}{2}$=7a4=35，
故选：B．

点评 本题考查等差数列的前n项和的性质，解题的关键是正确运用等差数列的性质以及前n项和公式．

练习册系列答案
相关题目
2．设单位向量$\overrightarrow{{e}_{1}}$，$\overrightarrow{{e}_{2}}$的夹角为$\frac{2π}{3}$，$\overrightarrow{a}$=$\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$，$\overrightarrow{b}$=2$\overrightarrow{{e}_{1}}$-3$\overrightarrow{{e}_{2}}$，则$\overrightarrow{b}$在$\overrightarrow{a}$方向上的投影为（　　）
A．-$\frac{3\sqrt{3}}{2}$B．-$\frac{2\sqrt{3}}{2}$C．$\frac{2\sqrt{3}}{2}$D．$\frac{3\sqrt{3}}{2}$
15．已知M为△ABC所在平面内的一点，且$\overrightarrow{AM}=\frac{1}{4}\overrightarrow{AB}+n\overrightarrow{AC}$．若点M在△ABC的内部（不含边界），则实数n的取值范围是（0，$\frac{3}{4}$）．
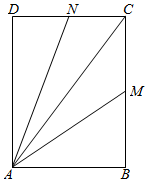12．如图，矩形ABCD中，AB=3，AD=4，M、N分别为线段BC、CD上的点，且满足$\frac{1}{C{M}^{2}}$$+\frac{1}{C{N}^{2}}$=1，若$\overrightarrow{AC}$=x$\overrightarrow{AM}$+y$\overrightarrow{AN}$，则x+y的最小值为$\frac{5}{4}$．
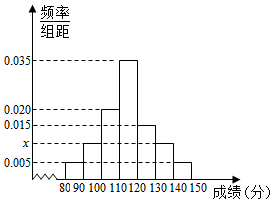19．40名高三学生某次数学考试成绩（单位：分）的频率分布直方图如图：
（Ⅰ）求频率分布直方图中x的值；
（Ⅱ）分别求出成绩落在（130，140]与（140，150]中的学生人数；
（Ⅲ）从成绩落在（130，150]中的学生中任选2人，求此2人中至少有1人的成绩落在（140，150]中的概率．
9．执行如图所示的程序框图，若输入x的值为-5，则输出y的值是（　　）
A．-1B．1C．2D．$\frac{1}{4}$
16．正三角形ABC边长为2，M、N分别为边AB、AC的中点，点P为线段MN上的动点，则$\overrightarrow{BP}•\overrightarrow{CP}$的取值范围是[$-\frac{1}{4}$，0]；若$\overrightarrow{BP}=x\overrightarrow{AB}+y\overrightarrow{AC}$，则（x+1）•y的最大值为$\frac{7}{16}$．
13．设函数f（x）=x2+ax+3．
（1）当x∈R时，f（x）≥a恒成立，求a的取值范围；
（2）当x∈[-2，2]时，f（x）≥a恒成立，求a的取值范囤；
（3）设不等式f（x）≥a对于满足1≤a≤3的一切a的取值都成立，求x的取值范围．
14．若复数z1=3+4i，z2=1-2i，其中i是虚数单位，则复数$\frac{{|{z_1}|}}{i}+\overline{z_2}$的虚部为-3．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网