题目内容
10．等比数列{an}中，公比q=2，前100项的和为150．则a2+a4+a6+…+a100=100．分析 利用等比数列数列的前n项和公式即可得出．
解答 解：∵$\frac{{a}_{1}（{2}^{100}-1）}{2-1}$=150，
∴a2+a4+a6+…+a100=$\frac{2{a}_{1}[（{2}^{2}）^{50}-1]}{{2}^{2}-1}$=$\frac{2}{3}{a}_{1}（{2}^{100}-1）$=$\frac{2}{3}×150$=100．
故答案为：100．
点评 本题考查了等比数列数列的前n项和公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
20．“a=1”是“复数z=（a2-1）+2（a+1）i（a∈R）为纯虚数”的（ ）
| A． | 充要条件 | B． | 必要不充分条件 | ||
| C． | 充分不必要条件 | D． | 既不充分也不必要条件 |
5．若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1上一点与其左顶点、右焦点构成以右焦点为直角顶点的等腰三角形，则此双曲线的离心率为（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | 2 | D． | 2$+\sqrt{2}$ |
15．（1+x）n（3-x）的展开式中各项系数的和为1024，则n的值为（ ）
| A． | 8 | B． | 9 | C． | 10 | D． | 11 |
2．设单位向量$\overrightarrow{{e}_{1}}$，$\overrightarrow{{e}_{2}}$的夹角为$\frac{2π}{3}$，$\overrightarrow{a}$=$\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$，$\overrightarrow{b}$=2$\overrightarrow{{e}_{1}}$-3$\overrightarrow{{e}_{2}}$，则$\overrightarrow{b}$在$\overrightarrow{a}$方向上的投影为（ ）
| A． | -$\frac{3\sqrt{3}}{2}$ | B． | -$\frac{2\sqrt{3}}{2}$ | C． | $\frac{2\sqrt{3}}{2}$ | D． | $\frac{3\sqrt{3}}{2}$ |
11．设定义在（0，+∞）上的单调函数f（x）对任意的x∈（0，+∞）都有f（f（x）-log3x）=4，则不等式f（a2+2a）＞4的解集为（ ）
| A． | {a|a＜-3或a＞1} | B． | {a|a＞1} | C． | {a|-3＜x＜1} | D． | {a|a＜-3} |
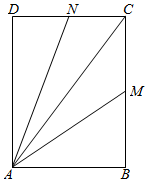如图，矩形ABCD中，AB=3，AD=4，M、N分别为线段BC、CD上的点，且满足$\frac{1}{C{M}^{2}}$$+\frac{1}{C{N}^{2}}$=1，若$\overrightarrow{AC}$=x$\overrightarrow{AM}$+y$\overrightarrow{AN}$，则x+y的最小值为$\frac{5}{4}$．