题目内容
10.函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则φ的值为$\frac{π}{6}$.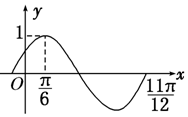
分析 由题意结合函数的图象,求出周期T,根据周期公式求出ω,求出A,根据函数的图象经过($\frac{π}{6}$,1),求出φ即可.
解答 解:由函数的图象可知:$\frac{3}{4}$T=$\frac{11π}{12}$-$\frac{π}{6}$=$\frac{3π}{4}$π,
T=π,所以ω=2,A=1,
函数的图象经过($\frac{π}{6}$,1),所以1=sin(2×$\frac{π}{6}$+φ),
因为|φ|<$\frac{π}{2}$,所以φ=$\frac{π}{6}$,
故答案为:$\frac{π}{6}$.
点评 本题是基础题,考查三角函数的图象与性质,函数解析式的求法,考查计算能力,发现问题解决问题的能力.

练习册系列答案
相关题目
20.(x3+x)3(-7+$\frac{1}{{x}^{2}}$)的展开式x3中的系数为( )
| A. | 3 | B. | -4 | C. | 4 | D. | -7 |
1.设p:0<x<5,q:-5<x-2<5,那么p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
5.假设关于某设备的使用年限x(年)和所支出的维修费用y(万元)有如表的统计资料:
若由资料可知y对x呈线性相关关系,试求:
(1)线性回归直线方程;
(2)根据回归直线方程,估计使用年限为20年时,维修费用是多少?
回归直线方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$的系数为:$\left\{\begin{array}{l}{\stackrel{∧}{b}=\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}}\\{\stackrel{∧}{b}=\overline{y}-\stackrel{∧}{b}\overline{x}}\end{array}\right.$.
| 使用年限x(年) | 2 | 3 | 4 | 5 | 6 |
| 维修费用y(万元) | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(1)线性回归直线方程;
(2)根据回归直线方程,估计使用年限为20年时,维修费用是多少?
回归直线方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$的系数为:$\left\{\begin{array}{l}{\stackrel{∧}{b}=\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}}\\{\stackrel{∧}{b}=\overline{y}-\stackrel{∧}{b}\overline{x}}\end{array}\right.$.
19.已知f(x)=xn,若f′(-1)=3,则n的值为( )
| A. | 3 | B. | -4 | C. | 5 | D. | -5 |